電気力線

内容：「電界」を、各点での方向に、なぞって繋げて、向き付きの線にしたもの。

目的：「電界」の性質を「場の方程式」を使わないで理解するために、便宜的に用いる。

限界：主に時間的な変化のない静電場に適用する。拡張は可能だが、話が難しくなる。

コメント：髪の毛のような実在する線ではないので「一本」に対する特別な意味はない。

性質：
＜物理的性質＞
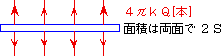
１、電荷Ｑ[C] に対して、４πｋＱ[本] の電気力線が繋がる（ｋはクーロンの比例定数）

２、電気力線と垂直な小さな面を貫く単位面積当たりの本数が電界の強さと同じになる

３、隣り合う力線同士は互いに反発して均等に広がろうとする（圧力）
４、力線自身は縮もうとする（張力）

＜数学的性質＞
５、分岐しない。電荷の無いところでは途切れない。

６、向きがあり、プラスの電荷から、マイナスの電荷へと向かう
７、接線の向きが、電界の向きとなる

８、方向は、等電位面と常に垂直（つまり、導体の表面からは垂直に出入りする）
　（等電位面と電界は垂直なので、性質７と８は実は同じ内容です。）

問題

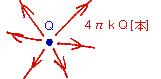
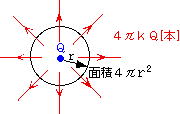例題：
電荷Ｑ[C] を帯びた大きさの無視できる小球がある。小球から距離ｒ[m] だけ離れた点での電界の強さを、電気力線の性質を用いて求めよ。
答え：
小球から距離ｒ[m] だけ離れた「点」を集めると球面になり、その面積は４πｒ２。その球面を、球面とは垂直に、４πｋＱ[本] の電気力線が貫く（性質１、５）。電気力線が互いに押し合って均等に広がろうとすることから（性質３）、球面上での力線の分布が均等になるので、電界の値は球面上のどこでも同じ。よって電界の強さは力線の本数を面積で割って（性質２）、
　電界 Ｅ＝（４πｋＱ）／（４πｒ２）＝ｋＱ／ｒ２

問題１：
電荷Ｑ[C] を帯びた半径Ｒ[m] の導体球がある、導体球の外側表面付近の電界の強さを求めよ。
ヒント：性質１、２、３　参照

問題２：
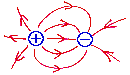
プラスの電荷同士が反発し、異符号の電荷が引き合う事を、電気力線の性質を用いて説明せよ。
ヒント：性質３、４、６　参照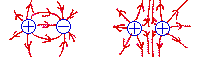

問題３：
電気を帯びた導体では、尖ったところの周りに電荷が集まり、電界が大きくなる。その理由を電気力線の性質を用いて説明せよ。
ヒント：性質１、３、８　参照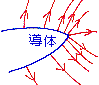
備考：尖ったところの電界が強くてなおかつ電荷が集まるために、尖ったところから、放電（＝電荷が飛び出す）しやすくなる。このため、たまった電荷を少しづつ空中に逃がすために、避雷針の先っぽは尖っている。トゲ付きの指輪をしておけば、ドアノブに触ったときにパチっと来ない。

問題４：
面積Ｓ[m２] の薄い導体板が一様に帯電している。全体の電気量がＱ[C] のとき、その板の表面付近の電界の大きさを求めよ。但し、(４πｋ)の逆数をε（＝「誘電率」という）とせよ。
ヒント：性質１、２、８　参照