問題提起
学校でのスタンダードな教えかたでは、
- 定義:
- 質量:天秤で測られる量
- 力:ばね秤で測られる量
と、した上で、(1)氷上を滑るおもりのイメージ、(2)台車を引く実験、(3)ばね秤どうしを引き合わせる、などの経験を根拠に、以下に示すニュートンの運動の三法則は「法則」であるとする。
- ニュートン 著(中野猿人 訳)プリンキピア「公理、あるいは運動の法則」より
- 法則1:すべての物体は、それに加えられた力によってその状態を変化させられない限り、静止あるいは一直線上の等速運動の状態をつづける。
- 法則2:運動(=運動量
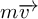 )の変化は加えられた動力(※)に比例し、かつその力が働いた直線の方向にそっておこなわれる。
)の変化は加えられた動力(※)に比例し、かつその力が働いた直線の方向にそっておこなわれる。
※ 動力:比例関係だけを扱うので、「力」と解釈しても良いし、「力積」と解釈しても良い。 - 法則3:すべての作用に対して、等しく、かつ反対向きの反作用が常に存在する。すなわち、互いに働きあう二つの物体の相互作用は常に相等しく、かつ反対方向へと向かう。
- 続けて、これらの公理(あるいは法則)から以下が導かれる。
- 系1:力はベクトル量として合成される(∵速度がベクトル量)
- 系2:力はベクトル量として分解される(∵合成の逆)/ついでに「てこの原理」も証明して傍証となす
- 系3:運動量保存則(∵第2第3法則)
- 系4:内力のみの質点系の重心の運動は第1法則に従う(∵運動量保存則)
- 系5:慣性座標系は互いに同等
- 系6:一様な加速を受ける加速度系でも、相対的な運動は慣性系と変わらず
☆ 運動の法則:この用語はニュートンによれば法則1〜3を指すが、高校物理では法則2のみを指す。本稿ではニュートンに従う。
しかしながら、ニュートンの運動の法則を公理ではなく「法則」とする順番には論理が複雑になってしまうという問題点がある。すなわち、
- 操作による定義の弱点:単純なものを定義するのに複雑な仕組みを必要とする。
- 天秤:てこの原理を利用して、重さを比較している。すなわち、質量の定義に「回転釣り合い」と「等価原理」が関わってくる。
- ばね秤:目盛りの割り振りの根拠となっているのは「フックの法則」とされている。フックの法則の意味を辞書で調べると、「力がバネの伸びと比例する法則」とある。
- 天秤とばね秤の動作原理の論理的な説明ができない:この方法では、純粋に論理としては、天秤とばね秤の動作原理を説明することを放棄したことになる。なぜならば、それが質量と力の「定義」になっているので、もしも動作原理を説明しようとすると論理の堂々巡り(トートロジー)になっていることに気づかされる。それはへりくつに見えるかもしれないが、その説明の内容から直感や経験を混ぜ込まないでロジックのみで冗長さを省いていくと最後には「質量は質量である。力は力である。」などに行き着いてしまう。
上記2つは、結局のところ同じことを述べていることにはなるが、互いに切り口を変えてみた。
経験から得られた直感によってワカッタつもりになるのであれば、質量と力を天秤とばね秤で定義するのも良いかもしれない。しかし、論理的な流れをつかもうとしたときに困難に直面する。そこで、ニュートンの運動の3法則を起点として、天秤とばね秤測られる量が、運動の法則に現れる質量と力と同じものであることを示せることを確認するべきである。
天秤
天秤とは、「てこの原理」を利用して、「重さ」の比を測定することにより質量を測定する装置である。ここでは、ニュートンの運動の3法則を公理として、天秤で質量が測られる動作原理を導くことができることを示す。ポイントは、てこの原理の証明と、重さから求められる質量が、運動の法則に現れる質量と区別できないことを確認することにある。
回転釣り合い(てこの原理)の導出
回転釣り合いに関しては、プリンキピア「公理、あるいは運動の法則」の中で、系2の説明の中でなされている。
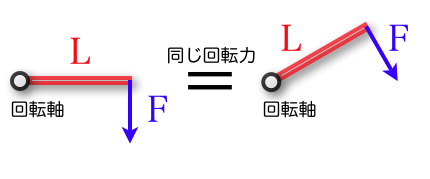
 釣り合いの関係の基礎 | まず、回転軸に対して垂直に延ばした腕の長さと、その先端に、軸とも腕とも垂直になる方向に加えた力の大きさが同じなら、回転はつり合う。 なぜなら、回転軸に対して、腕を回転させても、回そうとする力は変わらないので、
2つの腕を回して一致させれば、2力は大きさが同じで向きが正反対となり、相殺する。ゆえに回転力は得られない。 |
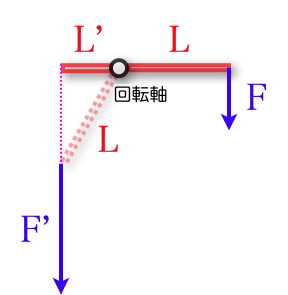 力を加える点を作用線上で移動 |
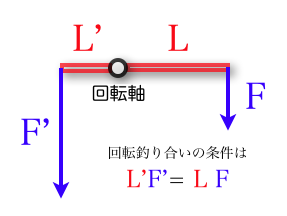
次に、腕の長さが異なる場合、つり合うための力の大きさを求める。
|
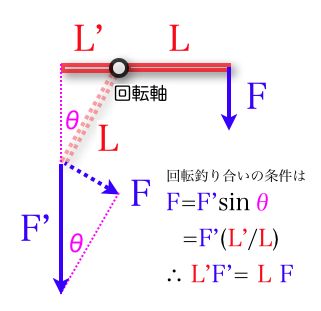 腕の長さが異なる場合の、釣り合いの条件 |
|
重力質量と慣性質量
- ニュートンの第2法則に運動量の定義を代入した式に現れる質量を「慣性質量」、
重さに比例する量として定義される質量を「重力質量」と呼んで区別する考え方がある。
この視点からは、天秤で測定されたのは重力質量であり、ニュートンの運動の三法則に現れる質量とは別物なのではないかという疑問が提起される。
- 物体の自由落下に関して運動方程式を立てると、a を加速度、g を重さと質量の間の比例定数として、
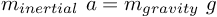
となるから、物体の落下の加速度は、物体ごとに、慣性質量と重力質量との比に依存することになる。 もし、この2種類に呼ばれている質量の比が物体によって異なることが示されたなら、ピサの斜塔の実験の逸話は嘘だったことになる。 - 自由落下では空気の抵抗も無視できず、実験の精度が悪い。手軽に確認できる実験としては、振り子を使う。振り子の周期は、振り子の長さを
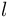 として、
として、

と、計算されるから、振り子の周期が物質の種類によらないことを検証すれば良い。 - ニュートンはプリンキピアの中で、振り子を使って検証したと述べており、十分に一致(比例)することを確認している。 プリンキピア冒頭に質量の説明が書かれてあり、そこでは質量とは「重さに比例する示量変数」とされているが、 慣性質量と重力質量の一致(比例)を十分に確認していなければ、重さでもって質量の意味を与えることには問題が生じたであろう。
- 一致の精度や、実験の歴史的経緯などに関しては、英語版の Wikipedia に詳しく書かれてある。 現在確かめられている精度は、10万トンタンカー10隻分の質量に対して、誤差は1円玉一個分にも満たない。
- オトナ実験で極めて高い精度で慣性質量と重力質量の一致をみているのだから、もはやコドモ実験では区別する必要など無いであろう。 もしも差異が認められたとしても、極めてわずかな修正が与えられるに過ぎず、学校の理科室で実験するような事例に影響を及ぼすことなど全く無い。
- この区別は物理的なものではなく、むしろ理論の組み立ての過程で生じた「形而上学」的な視点によるものであったとも考えられる。 しかし、疑う考え方が有る以上、徹底的に検証する価値はある。 たとえば、地球と月を合わせた質量は、地球単独の質量と月単独の質量から、重力による結合エネルギーを差し引いた分になるが、 これを確認するには高い精度が要求される。物質の組成ごとに重力の大きさが食い違っていてはいけない。 ゆえに、この場合は等価原理の検証実験が重要な役割を果たした。(ref)
- そうはいっても、「兎は兔とは異なる生物である」という仮説のもとで、兎と兔の違いを徹底的に調べてみた結果、 わずかな違いさえも見つからなかったとしたら、素直に兎と兔は同じ生物であったと結論づけるべきではなかろうか。
- 物体の自由落下に関して運動方程式を立てると、a を加速度、g を重さと質量の間の比例定数として、
- この問題を簡単に回避するためには、天秤を一定の加速度で加速する宇宙船の船内に持ち込めばよろしい。そうすれば、地球の重力は無いのだから、「重力質量」など、もともと関係無い事になる。なんら迷う余地も無く、重力と質量の関係は運動の法則で与えられることになる。
- 考え方としては、
- まず第1法則が成り立つような座標系、すなわち慣性系を用意するべきである。 その意味では地球に向けて落下し続けている宇宙船の船内などは、格好のデモンストレーションとなるであろう。 高校物理の視点からは、これは重力と慣性力がつり合っているからだと説明されるが、 それはあくまでも定期試験や受験へ向けて考え方を統一するためのもので、 重力と慣性力の区別など、○○原理などと名付けるまでもなく、物理的にはもともと存在しない。 この手の形而上学的な視点はひとまずよそに置いておくことにして、現象としては、3次元的に慣性系が用意されていることになる。 ただし、地球が作る自然重力と、座標系を加速して作りだす人工重力の違いは潮汐力の有無にあり、潮汐力が無視できる精度と範囲に限定する必要がある。 理科実験程度の精度と、宇宙船の船内程度の広さであれば、なんら問題となるところは無いであろう。 その上で、地球の方向に対して、反発や引き込まれる加速を示す物体が無いことを確認する。
- 次に、地球に落下し続ける宇宙船の船内で、ハコを地球から遠ざかる向きに加速する。すると、運動の法則により、ハコの中の物体は、ハコに対して「落下」する様子が観察されるであろう。
- そのハコの加速度を、宇宙船が地球を中心に回転する回転運動の加速度と一致させれば、ハコの運動は等速直線運動になるから、地球上に静止しているハコと速度と高度以外は変わらないことになる。
- 要するに、自由落下する大きなハコの中で、地球から遠ざかる向きに(つまり上向きに)加速度 g で加速する小さなハコを考えると、その小さい方のハコは、地上に静止する物体に対して静止または等速直線運動をしている。大きなハコを基準にして考えれば、振り子の実験などの事実を踏まえ、重力が運動の法則で説明できたことになる。
参考:質量標準
- 質量を測定するとは、基準となる質量の何倍かを定めることである。
理科室の実験程度の精度であれば、4℃の水1リットルを以て、1kg と見ることができる(※1)が、精度を上げるためには、もっと厳密な基準が必要である。そこで 1kg を定めた世界でたったひとつの「キログラム原器(※2)」なるものが用意され、厳重に保管されている。
※1. 1901年の第3回国際度量衡総会で1リットルとは「1気圧のもとで最大密度にある純粋な水1キログラムの占める体積」と定められた。 (ref)
※2. 1889年の第1回国際度量衡総会で1キログラムを、白金とイリジウムの合金である国際キログラム原器の質量と定義し、国際キログラム原器を国際度量衡局(BIPM)が保管することが決定された。 - しかしながら、キログラム原器では、汚れや錆への対応など、扱いが大変難しい。水1リットルのように、どこにでもあり、なおかつ精度の十分に高い標準が求められている。測定技術は進歩して、キログラム原器の汚れの有無程度よりも正確に測定ができるようになってきたから、物理定数のどれかを固定してしまうことにより、「1キログラム」の基準をブレなくすることが考えられる(※)。候補として特に有力なのは、以下の2つである ※ 2011年の第24回国際度量衡総会で、国際キログラム原器を将来廃止し、基礎物理定数によるキログラムの再定義を実施する合意がなされた。(ref)
- リンク:キログラム - Wikipedia
天秤のまとめ
天秤は、てこの原理を利用して重さの比を測定する装置であるが、てこの原理は、ニュートンの運動の法則から導出できた。 重さと質量が正確に比例することは、空気などの抵抗の無いところで万物が斉しく同じ加速度で落下する事実と照らし合わせると、これもニュートンの運動の法則から導出される。 ゆえに、天秤による質量の測定原理は、ニュートンの運動の法則から導出される。 よって、ニュートンの運動の法則を自然法則ではなく公理として扱う立場に立つならば、 天秤で測定されるところの「質量」の定義は、ニュートンの運動の法則(+ ニュートンの運動量の定義 mv )の中に含まれていると考えることが可能である。
ばね秤
教科書では、ばね秤の目盛りの振り方の根拠はフックの法則にあるとされている。 そしてフックの法則を辞書で調べると、バネの戻ろうとする力と伸びが比例する法則と書いてある。 コレでは堂々巡りになってしまう。フックの法則の原理を説明しようとすると、物性の話になり、物理の導入レベルの話ではなくなってしまう。 しかし、ニュートンの運動の三法則から、ばね秤の仕組みを説明する流れにすれば、論理はスッキリと整理されるであろう。
前提
バネが復元可能な範囲の伸びで考える。繰り返し使用しても、同じ力に対して同じ伸びを示す範囲で用いる。 金属疲労を考慮しなければならないような回数を使うことは想定しない。
単位1N
ニュートンの運動の三法則を前提とすれば、例えば、以下の方法で、力の単位を定めることができる。
- 摩擦の無い滑らかな床の上を 質量1kg のおもりが運動するとする。
- おもりには軽いヒモがついており、 おもりの重心から長さ1m のところでヒモは大きさと摩擦の無視できる滑車を通り、その先は、ばね秤へとつながる。
- 滑車はおもりと同じ高さであるとし、滑車からの距離が変わらないように注意しつつ、おもりを角速度
1 rad/sで回転させたとき、ヒモの引く張力を1 Nと定め、その時のバネ秤が指し示す位置を、目盛り1N として記録する。
∵ 第2法則T = m r ω2
目盛りの構成方法の例その1
- 目盛りのまだ割り振られていないばね秤を多数用意する。
- 基準となる一つの目盛りを割り振られたばね秤を一つ用意する。
- 基準となる一つの目盛りを割り振られたばね秤と、その他のばね秤と引き合わせることで、目盛り1をコピーする。(∵第3法則)
- ばね秤同士を総当たり的に引き合わせることで、目盛り1の位置があっていることを確認する。(第3法則確認 / 不良品がないか確認)
- ばね秤n本と、m本をそれぞれ均等に束ね、引き合わせることで、互いに
m/n,n/mの目盛りを割り振ることができる。(∵系1力の合成)
目盛りの構成方法の例その2
- 基準となる一つの目盛りを割り振られたばね秤を一本と、まだ目盛りの割り振られていないばね秤1本を用意する。
- ばね秤2本とヒモを互いに引き合わせ、ばね秤同士の角度は常に直角になるようにする。
- 基準となるばね秤の目盛りの読みは常に1になるようにし、ヒモの角度を定めることにより、残りのばね秤の目盛りを割り振ることができる。
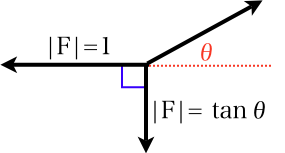
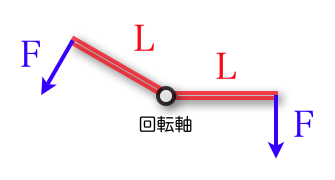
3力のつり合いを利用した、目盛りの割り振り。
ばね秤のまとめ
運動の第2法則から、基準となる力の大きさを定めることができ、ばね秤同士を引き合わせることにより、フックの法則を使わないで、第2法則から導かれた力の合成と第3法則のみで、ばね秤に目盛りを割り振ることができた。よって、ニュートンの運動の法則を自然法則ではなく公理として扱う立場に立つならば、ばね秤で測られるところの「力」の定義は、ニュートンの運動の法則の中に含まれていると考えることが可能である。
まとめ
学校では通常、質量と力は天秤とばね秤で測られる量であるとし、ニュートンの運動の三法則は、自然法則であると教えられる。しかし、プリンキピアに習い、ニュートンの運動の三法則を公理とする立場で考えれば、天秤とばね秤での質量と力の測定原理を定めることができるから、この方針のもとでは質量と力の定義はニュートンの運動の三法則の中に含まれていると考えることができる。