p43 Physical states

Number oprator

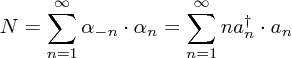
(2.97)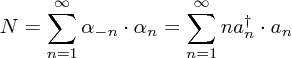

とすると、Nとの交換関係が

と計算されるので、整数値を固有値に持つ。 は「k 番目の振動モード」の固有状態(?)。質量の固有値に比例するのではなく、質量の自乗の固有値に比例するのはなぜ？エネルギーは振動数とプランク定数の積の合計にはならないの？ Q:これをどう考える？ ⇒金属の箱の中の電磁波の振動モードの様なものとは、違うらしい。

Closed string , Level matching

閉弦の場合、classical には

(2.83)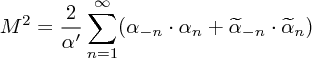

である。これにより、

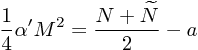
と、するべきであるようには見えるが、( 2.40 - 41 ) で X_R , X_L の σについての一次の項のウエイトを同じ（足してσの１次の項をキャンセル）にしたので、　L_m を求める式 (2.81) は左回り^〜についても同様に成立。よって、拘束条件　　は、

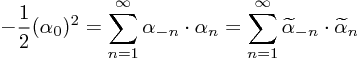
となる。並びに、(2.42) (2.46)

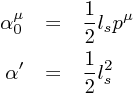
より、

(2.98)

としてよい。

“level-matching condition” :

Virasoro generators and physical states

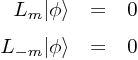
だとすると、量子版の Virasoro algebra (2.93) によれば、

となるから、(2.95) より、

で、なければならない。a, c が、0 ではない m に依らない定数であるとするならば、この式の成立は無理で、全ての L_m に対して。

とすることは不可能と言える。よって、この条件を正の m にのみ課す事にする。負の m についてはエルミート共役。

？？　 とかしないのはなぜ？

⇒もしかしたら、m=1 ぐらいで可能な選択肢ができるかもしれないね。