といった形の面積で作用を与えるのが Nambu-Goto Action (⇒2.11)。しかしこれでは場の量が２次形式にはならないので、量子化するための指針が見つけられない。そこで、測地線の方程式に対して行われる手法を導入してみる。ヒモが描く世界面を部分空間として、その世界面内の座標に対するメトリック hαβ を未定定数扱いにして、作用を作ってみる。
これまでは、規格直行座標を選択するという意味でのゲージ固定しか行っていなかった。電磁場にたとえるならば、局所ローレンツ変換の対称性を残したローレンツゲージの様な扱い。これを、ローレンツ変換に対する共変性を捨て、conformal factor も固定し、電磁場でのクーロンゲージのような扱いに変えることによって、積極的に拘束条件を解いてみる。力学変数から、時間方向成分を除外するから、負ノルムの問題が回避されると期待される。
古来、力学の法則を記述するのに、点粒子が 1 + (D-1) 次元内に描く世界線を扱ってきたが、量子論的な動機により、これをヒモが、 1 + (D-1) 次元内に描く世界面を扱うことにした。作用量は、世界線上の固有時の合計から、世界面上の面積の合計へと修正される。
面積 |A×B| を計算するに当たり、2つのベクトルの内積(A・B)と外積(A×B)の二乗和が、それぞれ自身の内積の二乗の積に等しいことから、
といった形の面積で作用を与えるのが Nambu-Goto Action (⇒2.11)。しかしこれでは場の量が２次形式にはならないので、量子化するための指針が見つけられない。そこで、測地線の方程式に対して行われる手法を導入してみる。ヒモが描く世界面を部分空間として、その世界面内の座標に対するメトリック hαβ を未定定数扱いにして、作用を作ってみる。
世界面の記述は、背景時空の座標を大文字の Xμ , 世界面上のローカルな座標を σα で表すことにして、関数の組 Xμ(σ) として与えられる。
任意の点の近傍で、
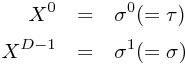
なるような規格直交座標を選ぶことができるから、 hαβ が部分空間上のメトリックである限りは、常に、
でなければならない。これを拘束条件として扱えば、作用の中の密度要素である平方根に含まれる部分の中身は未定定数 h のみで構成されることになり、平方根の中に顕わには力学変数を含まないことになる。これが Polyakov action (⇒2.14)。
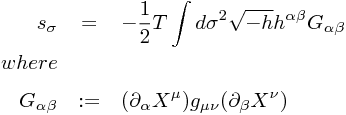
以後、これを扱う。
このやり方で運動を解くことは、X に対する運動方程式を、h が未定定数であることに起因する拘束条件のもとで解くことになる。
なお、仮に、hαβ = Gαβ とするならば、
により、Polyakov action は Nambu-Goto action に帰着する。
簡単のため、背景時空({g,X})はフラットであると、仮定すると、Polyakov action で
運動方程式は、
拘束条件は、
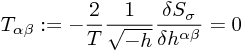より、
である。（つまり、Gαβのトレースフリーパートがゼロ。２次元の特殊性は使っていない。）
これらを解く手続きとしては、運動方程式の一般解を与えておいて、拘束条件をその解に課して、解の範囲を縛る。
2次元の世界面の場合 conformal 変換で、フラットな時空になれるから、世界面上の計量を、フラットな計量にconformal factor を付け加えたものにしても、（一般座標変換の範囲での）ゲージ固定ということ以外には一般性を失わない。（※ 教科書には conformal factor f につき、あらわには書かれていない。これは今野による「解釈」。）
この計量のもと、運動方程式は、単純な波動方程式となる。
上記の条件のもとで、運動方程式を解き、ヒモの長さが有限であることから、フーリエ展開し、正準交換関係を、フーリエ係数の間の交換関係に帰着させる。拘束条件の Tαβ のフーリエ係数 Lm が作る代数は、Virasoro 代数と呼ばれている。
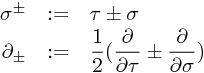
と定義すると、{ σ+ , σ- }を独立変数の組と見て、
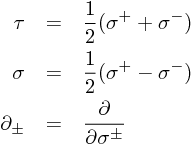
である。(2.33, 2.34)
計量は、
より、
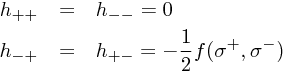
任意の増加関数を使って、ヌル座標 σ± をリパラメトリゼーション(2.126)
しても、計量に対するコンフォーマル変換と、局所ローレンツ変換に帰着されるから、
運動方程式も、拘束条件 Tαβ = 0 も、式の形が変わらない。この座標変換に対するゲージ固定は、2.4章までの正準量子化では行われていない。局所ローレンツ変換とconformal変換の対称性を残しているから、それらの共変性を残している代わりに、それだけ拘束条件を多く必要とする。解をフーリエ展開して得られたフーリエ係数は、これらも含めて Virasoro gererators Lm = 0 によって押さえられている。
▷ 運動方程式の解は、
で、与えられる。ヌル座標はそれら自身の任意の増加関数と置き換えても良いから、ゲージ固定という意味で、この中の成分の一つを、手で入れたσ±の関数で与えることが可能である。
▷ 拘束条件のうち、 T+ - と T- + は、自明にゼロ。ほかは、
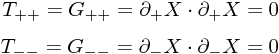
となる(2.36, 2.37)。これらは、49ページ中程で、Virasoro constraints とも呼ばれている。
簡単のため、背景時空の座標 Xμ にも null 座標を導入してみる。ヌル座標の添え字は、{0 , D-1} の代わりに {＋ , −}とする。
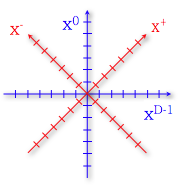
すると、拘束条件（Virasoro constraints）は、μ= 0, D-1 の部分を書き下して、
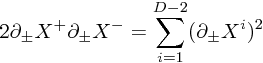
と書かれる。
背景時空の座標値の成分の内の一つ：X+R , X+L がそれぞれσ±の単調増加関数または単調減少関数であると仮定するなら、σ± を適宜リパラメトライズして、
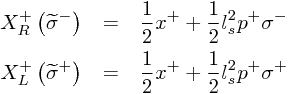
と、することができる。これで、ローレンツ変換とconformal factor を gaube固定したことになる。
この条件のもとで、拘束条件（Virasoro constraints）は、
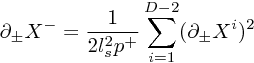
となる(2.132)。つまり、クラシカルには、X- は、力学的な変数から外れ、積分されて他の量から与えられることになる。
Open string の場合、ヒモの端（σ=±½π）の条件から制限が効いて、
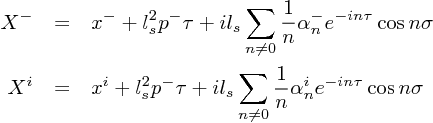
と、書かれる(2.133)。各モードの係数 α は、ポアソン括弧により、代数が決められる。これらを拘束条件に代入して、解
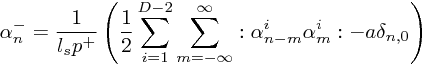
を得る(2.134)。これで、light-cone gauge において、拘束条件が解かれて、X± を力学的な自由度から消去することができた。
(2.132)によれば、
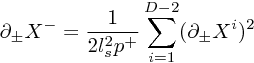
とのことで、ホントに可積分なのか、確認したくなる。計算してみたところ、
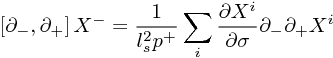
なので、Xi に関して、運動方程式が満たされる限りにおいては、可積分であることが保証されている。
！: 量子論的にはどうなのか、きちんと詰める必要があるかもしれない。
何とか図にかけないものだろうか？
空間的な意味で円く輪になっていると、「ひとまわり」に対して、X+L , X+R が、σ±の単調増加関数できるとは考えられない。丸くなっているせいで、XD -1 の値の増加に対して、２つに分岐し、片方は増加、片方は減少という形になるはず。これをどう考える？XD -1 が、円筒座標の角度のようになっていたら、可能かもしれないけれども、そうすると、規格直交座標ではなくなってしまう。どうする？
世界面の中で、X0-XD-1 面と平行な面ができると、そこのタイムスライス線が null になってしまう。どうする？必ず Xi 方向にドリフトすると考えるか、世界面の XD-1 方向への広がりは無いと考えるか...？
もしかして、空間方向の次元を勝手に一つ増やして、時間と対にして扱えば、常に拘束条件を解いた形に持ち込める...ということか？
Copyright © 2009 Shigeru Konno All Rights Reserved.
[INDEX | 印刷用(Safari)]