p40 2.85 Weyl 変換の対称性

計量の Lie 微分

Gauge 変換  により、

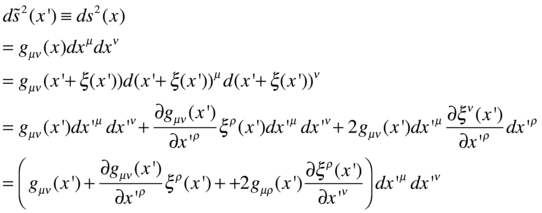
よって、計量のLie微分は

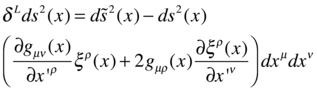
ゆえに、成分で表示するなら、以下のようになる。

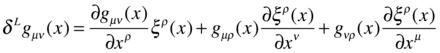
この値がゼロになれば、ξ方向に時空は対称。（⇒ Killnig vector）

Weyl変換とLieドラッグ

gaugeの選択 hαβ=ηαβを、ストリングの世界面上でグローバルに選択できたのは、Weyl 変換不変性を利用して世界面の曲率をゼロにすることができたから。まだ、Weyl 変換不変性に対応した拘束条件が残っているに違いない。conformal factor は場所毎に異なって良いから、世界面上をベクトルξ向きに微少な移動をした際に、conformal factorのズレΛが見いだされるはず。ξ方向への計量のLieドラッグが、Weyl変換になっていた場合、

より、

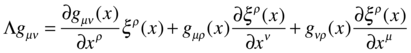
が成り立つはず。

それで、？

つまり(2.85)式

が、成り立つ。非対角成分とトレースがゼロだから、

これを並び替えて、

ここで、

だから、ξ⁰+ξ¹ は σ- ≡ τ-σ の関数。 ξ⁰-ξ¹ は σ+ ≡ τ+σ の関数。

以上です