(BUTURIサークルほっかいどう サークルニュース投稿記事より)
| 実施日 | : | 1999年3月7日 |
| 参加者数 | : | 14人(高校教員1名、高校2年生12名、私) |
| 講義内容 | : | 相対性/慣性系 |
今回はDM宣伝作戦が功を奏し、新たに2校の先生がたに、ご協力をいただくことができ、参加者が増えました。ありがとうございます。参加者数は過去最高を記録しました。
今回の講義内容の範囲は、参加者が大幅に増えたこともあり、前回と同じとなりました。但し、前回だされた問題点を踏まえ、テキストは大幅に改良されています。また、積極的に実験と工作を試してみました。「相対性」の説明から入り「慣性の法則」「座標」「慣性系」「ガリレイの相対原理」「ガリレイ変換」・・・の順番で解説しました。
相対性の説明は、前回と同じく、単語の意味の説明から入り、位置や速度が相対的な概念であることを説明しました。ここは、すんなりと通り過ぎました。
慣性の法則と慣性系については、1ヶ月あまり、悩み続けていました。上下方向については、どう教えたらよいのか? 言い換えると、密閉された箱の中で、外部からの情報がないとき、重力又は慣性力が存在する座標系を、「慣性系」として導入することが妥当かどうか? 宇宙船の船内のように、等速直線運動が、触らなくても自然に観察できる系を教えるのが良いのではなかろうか? 高校物理では、「力が釣り合っていれば等速直線運動」というのが慣性の法則として許されます。これは「等速直線運動になるように外力を加えることができれば、慣性の法則が成立する」という詭弁を許す余地があります。培風館の物理学事典には「力が釣り合っていれば・・・」とは書いてありませんでした。事典は良く考えて作られています。ポアンカレは「科学と仮説」の中で、慣性の法則を「ひとつの物体の加速度は、この物体とこれに近接する諸物体の位置及びそれらの速度にしか依存しない」という記述に、一般化しています。まさに絶妙であります。様々な分野の人に教えを乞うたり、調べたり、考えたりするうちに、結局、自分は考えすぎだということがわかりました。上下方向については、生徒は言われなきゃ、わからない。光の湾曲だって目に見えないし・・・。
おまけに、多くの生徒は、等価原理を日常経験によって、とくに意識せずに、あたり前のこととして、受け入れているのだということも知りました。
そこで、慣性の法則については、上下方向については詳しく触れずに、なるべく水平方向について話をすることにしました。ドライアイスを滑らせて、実際に見せました。なんと、今までドライアイスを見たことがないという生徒もいました。机の上に砕いたドライアイスをバラ撒いて、机をいくら揺すっても、動かしても、ドライアイスの粒の間の相対的な位置関係は変わらない。・・・となるハズだったのですが、失敗しました。ドライアイスが滑りません。床に置いても滑りません。水分を含んでいるわけではないのですが、ザラメ雪のような構造をしており、細かく砕きやすい反面、すき間があるのでした。ドライアイスは、用途に応じて、買う店をよく選ぶべし!
つぎに、座標の説明です。意外にも、これは、ハマリます。物理的な実体と関連づけながら数直線を教えることは、簡単そうに見えて、実はとても奥が深かったのです。ある数学教育法の先生は「私もなかなか手が出せない」と、おっしゃっていました。かくして、テキストは、3回ほど全面的なリファインを受けました。「位相を入れる>距離を入れる>座標を規格化する」という手順の説明は、線路に駅を配置して、列車を通過させるというアイデアに行き着きました。しかし、講義を超特急で進めたために、生徒の反応は、残念ながら、よくわかりませんでした。改めて読んでもらったあとの感想が待たれます。
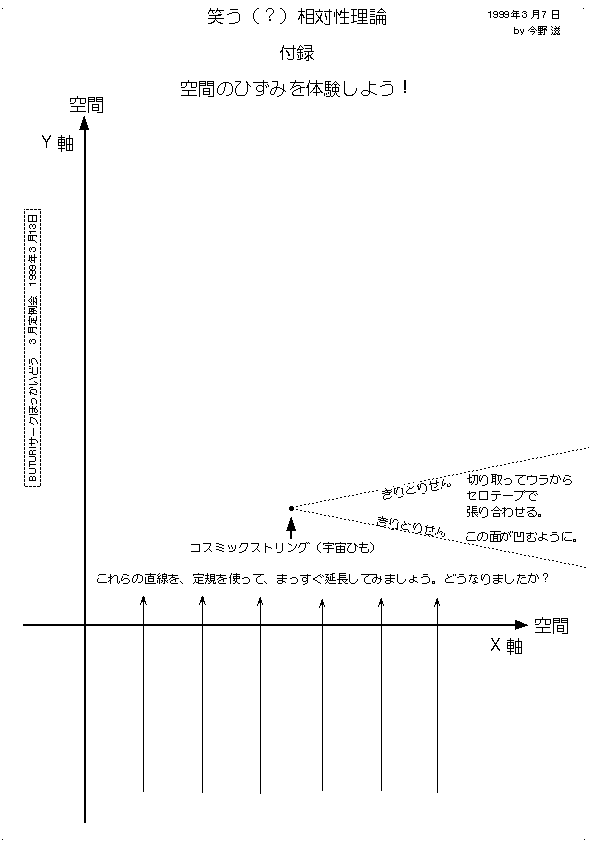
座標の1次元から高次元への拡張は、空間を薄くスライスしていくイメージで攻めました。これで個々の空間座標は数直線に帰着します。平面でスライス「できない」例として、コスミックストリングがある空間の例を挙げ、生徒に工作をやってもらいました。歪んだ空間があると「平行線が交わる」ことに、幾分よろこんでもらえたようです。ついでに、コスミックストリングや、宇宙項の質疑応答に花が咲きました。生徒のみなさんの宇宙に対する関心は高いようです。

コスミックストリングの議論の中で「このヒモは、つかめるのか?」という質問が出ました。考えてみたこともなかったです。高校生の素朴な感性にはあなどれないものがあります。コスミックストリングを構成している物質は、電磁相互作用をしないので、幽霊のように手をすり抜けることになります。但し「失われた角度」の効果で、手をつっこむと痛いです。
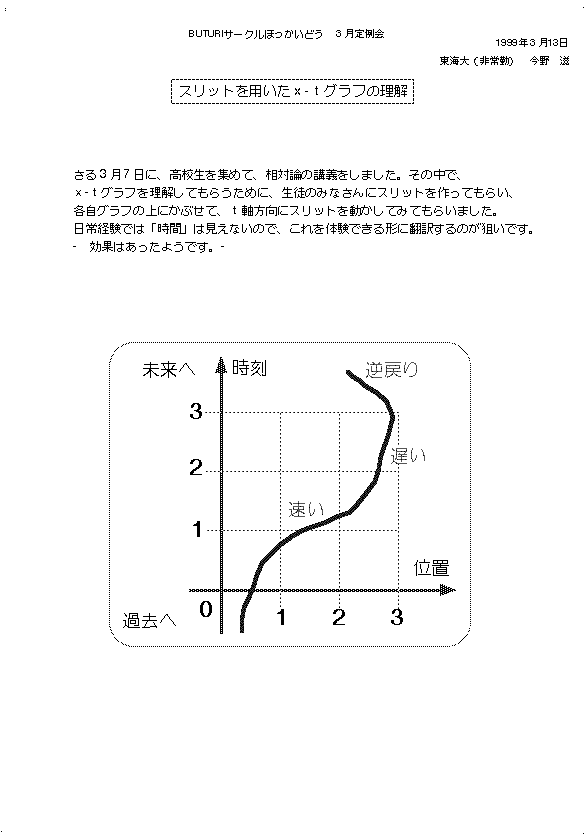
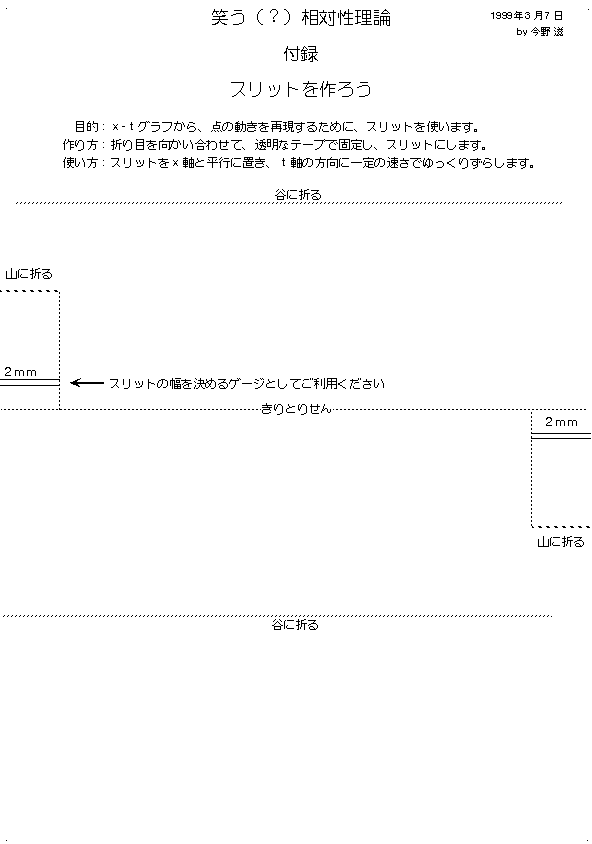
次に、x-tグラフの見かたの説明です。これは、ローレンツ変換を、グラフで理解するためには欠かせないステップです。点の動きとグラフの間の関係を、実感してもらうために、各自、スリットを作ってもらいました。すき間をx軸と平行に置き、スリットをt軸の方向に移動させます。意外にも「おー!点が動いてる!」とかいう反応がありました。成功のようです。
最後は時間切れとなってしまいましたが、「同時の相対性」に少しだけ触れました。
反省事項ですが、短時間に多くの内容を盛り込もうとした結果、かなり一方的に授業を進めた間があります。生徒からのフィードバックには、工作と実験では成功しましたが、講義については、失敗してしまいました。
Q:あなたの志望大学は?
A:理系が6人、文系が2人、その他不明。
Q:受講の動機(初めて来た人のみ)
A:興味があるから。/おもしろそうだから。/何となく。/科学雑誌に相対論が取り上げられており、気になっていたから。/学校の授業ではやられないから。/会場が学校に近いから。/相対論は自分でも本を買って勉強しているから。
重複して最も多い答えは、「興味」でした。
Q:講義の感想
A:話や説明がおもしろいので、時間があっという間に終わってしまった。/ドライアイスの件は少し残念。/自分としてはもっと進んで欲しかった。/人が多くて質問が多くてわかりやすかった。/宇宙ひもの話がおもしろかった。もっと詳しく知りたい。/面白くて、だんだん引き込まれていきました。/なかなか面白くて楽しかった。/知らない用語などがあったので、もっと勉強しようと思った。/よかった。/よくわからなかったけど、おもしろかった。/難しかったけど、実験はみんなが意見を言いあえて良かった。
Q:テキストの感想
A:読む時間がなかった。/前回よりも手が加えられている点が、とても良かった。(前回の参加者)/例が多くわかりやすい。/文のつながりが少し読みにくい。図式的にはっきりさせるべきだ。/読みやすい。/おもしろい。/読むのはキライ。/内容の展開については、もっと段階的にふくらませて、ひとりでも読める様なら、よりよいと思います。(先生のご意見)
改善すべき点についての意見もいくらか出ていました。参考にさせていただきます。
Q:問題編の必要性/受験との関連の是非
A:受験に関係があると、興味を失う。/問題は必要が生じたときにやればよい。/問題編はなくても良い。/無い方がテキストに集中できる。/今回のような小さなグループでは、問題編は無くても良いですが、大人数ではあった方がよい。(先生のご意見)/問題編と受験との関連は両方あった方がよい。/問題編はあった方がよい。
問題編に対するリクエストとしては、意見が大きく二分されているようです。
Q:学校の理科や数学の授業との関連がはっきりしていた方が良いですか?
A:無い方がよい。無い方が興味をもてる。/いいえ。/はい。/その方が良いとおもう。/その方が親近感がわく。しかし、ある程度やれば、はっきりしなくてもよい。/その時の内容に応じて、なるべくあった方がわかりやすいと思う。/おもしろければ、どちらでもよい。/ファインマン物理学のように、意識させないで、いつのまにか数学的な扱いになっているのが理想。(先生のご意見)
ここでも、意見が大きく二つに分かれたようです。
Q:何でもいいからひとこと
A:楽しかったのでまた参加したい。/次回もゼヒ!/男ばかりですごい。初めてだ。/自費で会場を借りるなど、行動的ですばらしい。/3時間の講義は長いと思ったけど、受けてみると短く感じた。/こういうことは、なんの役に立つのでしょうか?/羊は謎の動物だ。/etc・・・