2-4、光の速さは超えられるか? その2(速度合成)
ここでは、速度合成の法則(計算式)を導きます。 光の速さが光源と観測者の速度によらずに定数になるという事実から、 光の速さに近い速さで通り過ぎる宇宙船の中の時計の針の進みが遅くなることは知っています。 ならば、その宇宙船から打ち出された物体の速さは、宇宙船の中の人が測った速さよりも遅くなっているはずです。 つまり宇宙船から射出された物体の速さは、そのまま足されるわけではなく、小さく補正された値が加えられることになります。速さが加えられる様子を、ローレンツ変換を使って、きちんと計算してみましょう。
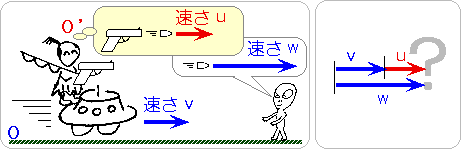
観測者のいる慣性系Oに対して、一直線上を一定の速さvで走り抜ける宇宙船があったとします。 その宇宙船の中から、宇宙船の運動方向と同じ方向に、小物体を射出したとします。 その小物体の速さは、宇宙船の中から見てuだとします。 このとき、観測者の測る小物体の速さがwだとします。 それぞれの速さの大きさが光の速さの大きさと比べて大変小さいときには、 ガリレイの速度合成の法則
w=u+v
が成り立ちます。uもvも光の速さと比べて十分に大きなときはどうなるでしょうか?ローレンツ変換を使って計算してみましょう。この物体が、時刻0で、原点にいたとします。すると、物体の位置は、
原点○ から測ると時刻t で、 x =wt
原点○’から測ると時刻t’で、 x’=ut’
と、表されます。このx、x’をローレンツ変換 [ 2-3-3節(4)式 ] に代入して、
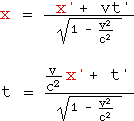 |
代入 ⇒ x ←wt x’←ut’ |
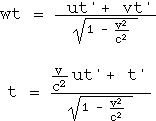 |
と、なりますが、上の式の両辺を下の式の両辺で割って、約分して、
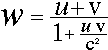
を得ます。これが速度合成の法則です。wは、速さvで走っている慣性系から、速さuで物体を射出した速度を意味しています。この式は、ガリレイの速度合成の法則とは、ずいぶん違って見えます。しかし、uやvの値がcに比べて充分小さければ、分母はほとんど1となり、ガリレイの速度合成の法則との区別がつかないでしょう。私たち人類の乗り物や輸送手段の速さは、光の速さと比べると、比較にならないほど遅いです。従って、日常経験できるような速さでは、ガリレイの法則で充分といえます。
ところで、少しづつ何回も速度を継ぎ足していけば、光の速さを越えることが出来るでしょうか?試しに、光の速さcから、合成された速度、wを引いてみます。通分して、分母と分子にcを掛けて以下の式を得ます。
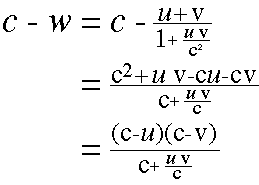
この引き算の結果から明らかにわかることは、uもvも共に光速に満たないならば右辺は正の値となり、左辺も正。 すなわち、wは光の速さに満たないことを意味しています。 ロケット噴射などの、人間がなし得る技術では、光の速さよりも遅い速度でしか、物体を打ち出すことが出来ませんから、どんなにがんばっても、この理論の適用できる範囲では、光の速さを越えることができないことを意味しています。
では、u=cだったらどうでしょうか? このとき、wの値もcとなります。
光の速さが、何処から見ても同じ値cをとるようにしたのだから、当たり前の結果です。
しかし、この事実はまた、光の速さで移動するものから、進行方向に打ち出されたものは、
やはり、光の速さになるしか無いという事実も示しているでしょう。
さらに、u>c、v<cだったらどうでしょうか? このとき、wの値もcを越えてしまいます。光の速さよりも、早い速度で移動する物体が、もし、あったとすると、それは、光より遅い速度を足しても引いても、光の速さよりも遅くなることは出来ません。
くどいようですが、これらの結果は、「光の速さは、光源や観測者の速度によらずに一定の値になる。」という実験事実から導かれたものです。
ここで、私たちは、一直線上を運動する物体の、
●速度合成の法則
について知ることが出来ました。
参考:公式の変形
tanh(x) = (ex - e-x)/(ex + e-x)
e = 2.71828…(⇒ネピア数)
という関数を使って、
u = c tanh(α)
v = c tanh(β)
と置くと、速度合成の式は、
w = c tanh(α+β)
と、とてもシンプルな形に書かれます。tanh(x) のグラフをあらかじめ書いておけば、合成される速さを作図で求めることもできます。この速さに関連した値 α,βは速度パラメータと呼ばれています。
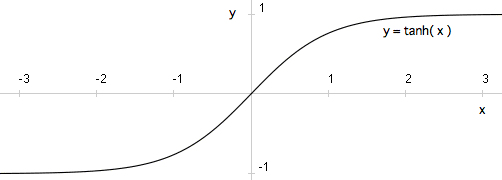
なお、tanh は「ハイプボリックタンジェント<Hyperbolic Tangent>」と読みます。(⇒双曲線関数)
問題1:慣性系に対して一様な角速度で回転する円盤のフチの速さは?☆☆
インターネットの掲示板などに繰り返し登場する超光速ネタとして、「長い棒を振り回せば、先端は光速を超える!」とかいう議論があります。それの答えもまた様々傑作で、半径が縮むんだとか、加速度を扱うのだから特殊相対論では扱えないだとか、珍案が飛び交います。これはおそらく加速度を扱うにあたって漠然とした躊躇があるせいだと考えられます。これはもちろん特殊相対性理論の範囲の問題で、本節の速度合成の式で簡単に計算できるのでした。物体の加速度を扱う際に、物体の速度と同じ速度を持った慣性座標系を使えば、速さはゼロか又はとても小さな値になるから、光の速さうんぬん言う前の普通の加速度の扱いに帰着できるのです。
ただし、実際に値を求める計算をするには「分数の積分」ができなければなりません。高校生と文系の大学生のみなさんには、敬遠されてしまいそうですが、考え方や話の道筋だけは把握していただきたいと思います。もちろん、理系の大学生のみなさんは、この計算ができないと、かなり恥ずかしい(2年生に進級する資格なし)です。
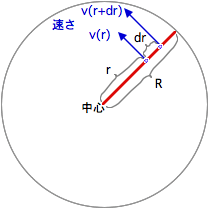
光の速さをc,円盤の半径をR,慣性系に対する円盤の角速度が円盤上のどこでもωであるとして、円盤のフチの速さを求めてください。
- 解法のヒント
- 円板状のすべての部分を同時に眺めると、至る所違う速度で、加速度もあり、おそらく途方にくれると思います。そこで、円盤上の勝手に選んだ点とその周りの点だけをまず考えることにして、その辺のの問題を解決してから、そこから全体に広げていきます。
- 円盤上の各点は加速度を持っているので、適当に選んだ円盤上の一点と常に共に動くような慣性座標系を選ぶことはできません。 しかし、勝手に選んだ或る時刻の前後の、とても短い時間に限り、その円盤上の一点と同じ速度で移動する慣性座標系を選ぶことができます。 ちょうど、走っている自動車のタイヤの表面が地面に対して、ほんの一瞬だけ静止するのと同じ理屈です。 慣性座標系が一瞬だけくっついて離れるので、この考え方を、仮に touch & go と呼ぶことにしましょう。
-
- 角速度とは
- 角速度には向きと大きさがあります。
- 角速度の大きさは、点が回転する回転方向の速さを回転の半径で割った値です。かけ算で表すならば、角速度の大きさに回転の中心からの距離をかけると、回転方向の速さになります。 速さが一定の円運動の場合は、回転の速さは、一周の長さを回転の周期で割った値になるから、 角速度は、弧度法で表した一周の角度2π(rad)を回転の周期で割った値と同じになり、 これは一秒間あたりに回った角度を表しているから、角速度と呼ばれています。
- 回転運動では動く点の描く円弧と回転の中心の両方を含む面を決めることができます。その面と回転の方向を合わせて、角速度の向きと呼びます。例えば、紙の上にペンでぐるぐる円を描いたときに、その紙の面が向いている方向ということです。縦×横×奥行きといった3次元空間の中での回転では、右ねじを回した時に右ねじが進む向きとして、矢印のように表現することもできます。(注意:矢印で表現できるのは3次元の場合のみ。時間も加えた4次元で考えるときには、矢印を使った表現は不適。)
- 一様な角速度とは、どこを回転の中心に選んでも、選んだ中心近くの点の運動の角速度が、一様に同じ値になることを意味します。このとき、角速度の大きさは、選ばれた回転の中心の点に touch & go する慣性座標系にて算出します。このとき、角速度の値は、円盤の中心に対する速さを円盤の中心からの距離で割ったものでは無いことに注意してください。なお、円盤上に引かれた直線は、その直線上のどの点の周りでも同じ角速度で回るのだから、曲がらずに、直線であることが保たれていることになります。つまり、一様な角速度で回転する円盤というのは、剛体(=変形の大きさを無視して良い固い物体)でできた円盤と言い換えても良いです。
- 慣性系にて運動する棒は、進行方向にはローレンツ収縮によって縮みますが、速度と垂直な方向には縮みません。なぜならば「同時の相対性」絡みでいわゆる相対論的な修正を要したのは進行方向のみだから。円盤が回転するとき、中心から外側に向かう半径の方向と、円板上の点が運動する方向とは垂直なので、半径方向に縮んだりしません。
- 計算を始める前に予想を立てよましょう。光の速さに近い速さで通り過ぎる宇宙船の船内の時計はゆっくり時を刻むように見えるから、その宇宙船の中で回っているコマも手許で見るよりはゆっくり回って見えるはずです。円盤のフチに近づくに従って速さは大きくなるから、その上に乗っている時計の動きもゆっくりになり、その点の周りの回転もゆっくりになります。つまり、フチに近づくにつれて角速度が小さくなっていくように見えるはずです。その結果、円盤上に引かれたまっすぐな線は、「同時の相対性」に由来する時間差のせいで、渦巻き状に巻かさっていくはずです。
- 計算
- 光の速さをc,円盤の角速度をω,中心からの半径がrの点の速さを
v(r)とすると、半径rの点に touch & go する慣性座標系から見て、その点のすぐ外側の半径r+drにある点は角速度ωで回転しているから、速さがωdrだけ増える。よって、速度合成の式は、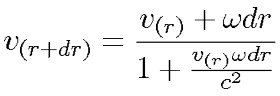
となるから、これを整理して積分する。積分定数は、v(0) = 0で決定される。 - 整理して、
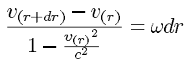
積分して両辺をcで割ると、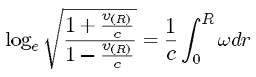
- 光の速さをc,円盤の角速度をω,中心からの半径がrの点の速さを
- 答え
- 光の速さをc,円盤の半径をR,円盤の角速度をωとすると、円盤の縁の速さは、
c tanh( ωR/c ) - ある瞬間に円盤上に引かれた中心を通る直線は、ぐるぐる渦巻きになっていくことになります。これは時間差があるせいでそうなるので、線の上の一点を選んで、その上に張り付いて線を観察した場合、その点の周りで、線は曲がっていません。
- 或る時刻に円盤上に引かれた直線ののアニメーション:

- 光の速さをc,円盤の半径をR,円盤の角速度をωとすると、円盤の縁の速さは、
問題2:地球上で物が落下するのと同じ大きさの加速度で加速し続ける宇宙船の1年後の速さは?☆
スタートレックなどのSFドラマに出てくる宇宙船は人工重力によって、人は浮かぶことなく地球上と同じような生活を送っています。しかしながらそのように便利に重力を制御することはおそらくできないものと考えられます(できたらすごいですが)。では、私たちが宇宙船内で浮遊せずに、地球上と同じ生活を送るにはどうすれば良いのかと申しますと、宇宙船本体を常に加速する方法が考えられます。ちょうど、車が走り出すときに体が後ろに押し付けられるのと同じ原理で、地球上で物体を自由に落下させる時と同じ加速度にて、宇宙船を加速し続ければよいのです。そうすれば、加速方向と反対向きに体が押し付けられて、つまり頭が加速方向を向く形で、地上同様に立って歩くことができます。クルーたちにとっては宇宙船の船首が「上」になるので、スタートレックとは向きが90°ずれることになります。
加速度とは、一秒間あたりの速度の変化ですから、単純に考えると、速度の変化は、加速度と時間の積で表されます。地球上で物体が自由に落下する加速度と同じ加速度で物体を、速さゼロからはじめて1年間加速させた場合、単純にかけ算で計算すると、光の速さを超えてしまいます。実際には光の速さのおよそ何%に達するのか、速度合成の式を使って計算してみてください。
- 計算
- 地球上で物体が自由に落下するときの加速度(=1秒間あたりに増える速さ)はおよそ、
9.8m/s2ですが、これを記号でgと置きます。宇宙船内の時刻を記号tで表し、とても短い時間をdtで表すことにします。時刻tでの宇宙船の速さをv(t)とすると、時刻t + dtでの速さv(t + dt)は、時間dtの間に加わる速さg×dtを速度合成の式にて加えて下記のようになります。
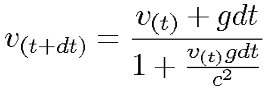
- これを前問と同じ要領で整理して積分して、始めの速さを0とした場合、
1年後の宇宙船の速さ=c×tanh( g×1年/c )
を得ます。 - 答え
- 約77%
