2-3、ローレンツ変換 導出編
19世紀末の実験結果によると、光の速さは、何処から見ても一定になることがわかりました。しかし、ガリレイ・ニュートンの相対性理論でいうところの速度合成の法則は、光に対しては成り立ちません。これに対して、様々な理論が提案されました。アイルランドのフィッツジェラルド ( George Francis Fitzgerald 1851-1901 ) と、電子の研究で有名なオランダのローレンツ ( Hendrik Antoon Lorentz 1853-1928 ) は、それぞれ独立に、空間そのものが進行方向に縮むとすると、つじつまが合うことを発見しました。さらにローレンツは、1904年、ガリレイ変換を修正し、2つの慣性系の間の時間も含めた変換(=座標の値の入れ替え)によって、力学ばかりでなく、電気と磁気の法則に関しても、同等に記述できることを示しました。この変換はローレンツ変換 ( lorentz transformation ) と呼ばれています。翌年、アインシュタインは、時間の概念も2つの慣性系の間では相対的になってしまうということなどを、整理されていて、わかりやすく解説した論文を発表しました。では、ローレンツ変換とはどんなものか、見てみましょう。
2-3-1、同時の相対性
光の速さが何処から見ても一定という、奇妙な現象によって、もっと奇妙な現象が引き起こされます。
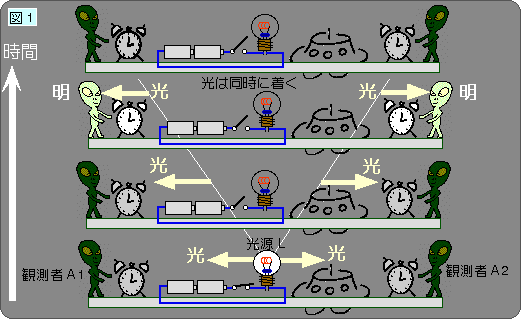
図1のように、慣性系(=ボールを転がすと、一定の速度で転がっていくような部屋と、位置を表す目盛の組)に固定された棒の両端に、観測者A1と、観測者A2を配置します。この二人の時計は予め正確に合わせておきます。棒の中央に光源を置き、一瞬だけスイッチを入れます。光源は真ん中にあるのだから、この二人の観測者が見た光の到着時刻は、必ず同じとなるでしょう。なお、図は、時間の順に下から上へと進み、4コマ漫画などとはさかさまの向きに並べられています。
一方、この図1のやりとりを、あなたが、棒に対して左向きに、速さvで移動して、観察したとしましょう。
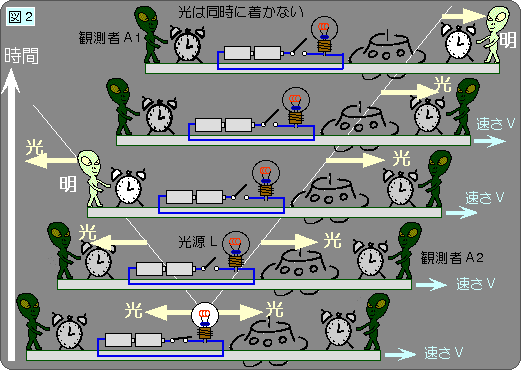
図2をご覧ください。あなたが見たA1(左)は、光へと向かっていきます。反対に、あなたが見たA2(右)は、光から逃げていきます。
多くの実験結果により、光の速さはどこから見ても一定でしたから、光は図2の場合でも、左右に同じ速さで伝わります。
光源LからA1とA2までの距離は同じだから、光は、向かってくるA1の方に先に着くことになります。 つまり、光の到着は、同時刻となりません。2人の観測者A1とA2から見たら、同時に起こっている出来事が、
走って見ると、同時ではなくなってしまっているのです。
言い換えると、棒の両端に固定した時計の示す時刻は、棒が目の前を走り抜ける場合、棒の後端の時計よりも先端の時計の方が「昔」を指し示すということがわかりました。
つまり、同時刻という概念は、慣性系ごとに異なってしまいます。
よって、2つの慣性系の間の座標変換(=位置や時刻を表す数字の割り振りの仕方の取り替え)は、光速度不変性まで考慮するならば、位置と時刻を別々に扱うことは出来なくなってしまっています。
|
練習問題:2人の観測者の間の距離は、棒を止めて測ったときにはLであったとします。図2で、後方の観測者に光がとどいてから、前方の観測者に光がとどくまでの時間を求めてください。但し、その時間は、見ているあなたの時計で測ったものとします。(これは難しいチャレンジだ!)
ヒント1>図2で、光が A1 にとどくまでの時間を t1、A2 にとどくまでの時間を t2 と置いてみよう。 ヒント2>図2での棒の長さは、ローレンツ収縮によって、Lよりも短くなっている。(1-3-2 章参照) ※ここの答えと同じ形が、ローレンツ変換で、またまた登場します。 |
2-3-2、アインシュタインの相対性原理
なぜか、ローレンツの理論よりも、後発のアインシュタインの理論が有名なので、ローレンツ変換を、アインシュタインの特殊相対性理論の中の一つとして位置づけて解説します。どちらの理論も、解釈こそ異なるかもしれませんが、導かれる結果は同じです。アインシュタインは、特殊相対性理論を構築するにあたって、以下の2つのことを仮定しました。(「特殊」が付くのは、扱う対象を、慣性系の間の関係に限定しているからです。)
| < 特殊相対性理論の基礎となる原理 > | |
|---|---|
| 相対性原理 | 互いに平行に等速直線運動をしている慣性系に対して、全ての物理法則は、同一の形式で表される。 |
| 光速度不変 の原理 | 光の速度は、その光源の運動のいかんに関わらず、全ての慣性系に対して同一の値 |
相対性原理については、ガリレイや、ニュートンと違う点は、「力学の法則」といっていたところを、意識的に「全ての物理法則」に書き直したところにあります。つまり、そのむかし未解明だった電気と磁気の法則についても成り立つようにしたことを強調しました。ただし、この「全ての」の意味は、現在の人類が知っている「全ての」です。その意味で、400年前には、力学の法則が「全ての」に該当したわけです。また、現在の「全ての」が400年後まで同じかどうかは、保証の限りではありません。
相対性といっても、なんでもかんでも相対的だというわけではなく、それぞれの慣性系で成り立つ物理法則自体は、絶対に変わりません。相対的な関係と、絶対的な関係を意識して区別しておいてください。
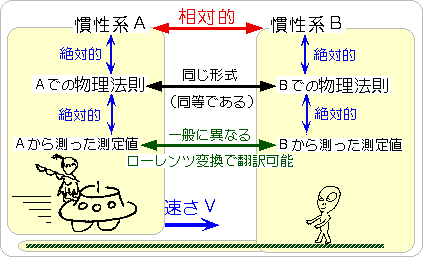
ここに、正確さを期するために、アインシュタインのオリジナルの言い回しを引用しておきます。よく用いられている表現と微妙に異なります。(日本語訳は文献1から引用)
| 電気力学の現象は力学の現象と同様に、絶対静止という考えを立証するような性質を持っていないように見える。むしろこれらの事実から、力学の方程式が成り立つ全ての座標系に対して、電気力学や光学の法則がいつも同じ形で成り立つと考えられる。このことは、小さな物理量の1次の近似については既に立証ずみのことである。
このような推測を第一の要請とみなして、相対性原理と呼ぶことにする。さらに次のような第二の要請をつけ加えよう。 光は常に真空中を一定の速さcで伝搬し、この速さは光源の運動の状態には無関係である。 これは、ちょっと考えると、第一の要請とは矛盾するように見えるかもしれない。しかしこれら二つの要請は、静止物体に対するマックスウェルの理論にもとづいて、運動物体の電気力学を簡単にかつ一貫して建設するためには充分である |
2-3-3、空間1次元の場合
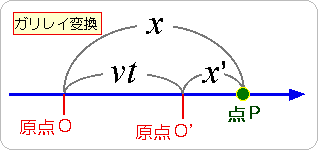
2つの慣性系の間の座標変換について考えます。てはじめに簡単のために、1方向にしか移動できない直線の世界を考えてみます。2つの慣性系から見た一つの点Pを表すのに、ガリレイ変換では、
としました。(2-2-4 参照)しかし、これは必然的に、ガリレイの速度合成の法則を導いてしまい、光速度不変の原理にマッチしません。原点Oから見ても、原点
そこで、原点Oとともに動く慣性系の時刻をt、原点
|
x =x’+vt’・・・(1-1)
x’=x −vt ・・・(1-2) |
なぜ、(1-1)に対して(1-2)が定まったかといいますと、
Oから見た
次に、光速不変の原理について検討します。時刻t=t’=0で、原点Oと
|
x =ct
x’=ct’ ・・・・・(2) |
これを(1)に代入すると、
|
ct =ct’+vt’
ct’=ct −vt ・・(3) |
となります。この両辺をそれぞれ掛け合わせると、
|
x =(x’+vt’)Cosh ・・・(1’-1)
x’=(x −vt )Cosh ・・・(1’-2) |
と置いてみます。これに(2)を代入すると、
|
ct =(ct’+vt’)Cosh
ct’=(ct −vt )Cosh ・・(3’) |
となるので、両辺をそれぞれ掛け合わせて、tt’で割り、
を得ます。これで、つじつまの合う式が作れました。むりやりに合わせなければならないような数も必要ありません。このCoshの符号については、
| v=0で、Cosh=1 → Cosh= | 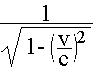
|
(1’-1)の右辺を(1’-2)右辺のxに代入して、tについて解き、以下のローレンツ変換が導かれます。
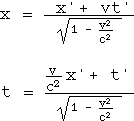
| }・・・(4) |
この式は、vがcに対して、とても小さな値であるときには、
|
(v/c)=0.1 なら、 Cosh=1.0050・・・
更に、x’=3m なら、(v/c2)x’=0.000000001秒 |
しかしながら、速さvが光の速さcに近づくと、大きな食い違いとなって現れます。
| 計算練習ですが、(4)を、x’とt’について解き返すと、vを これは、この式の左辺(又は右辺)の値が、vによらず、あらゆる慣性系で同じ値になることを意味しています。 |
ローレンツ変換のいろいろな表現
ローレンツ変換は、tの代わりに、ctでまとめて書くと、見栄えが良くなります。単なる見栄えで、特に深い意味はありません。
Cosh =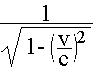 , Sinh =(v/c)Cosh , Sinh =(v/c)Cosh
と、置くと、ローレンツ変換は、 ct = ct’Cosh + x’Sinh x = ct’ Sinh + x’Cosh ・・・(4’) |
ここで、私たちは、空間1次元の場合の
