2-5、ローレンツ変換 図解編
2-5-1、グラフでナットク
ここでは、ローレンツ変換
自然法則は幾何学の言葉で記述される!?
物理学の醍醐味の一つは、自分が予言者になれることです。森羅万象の出来事が、時間と共にどの様に変化していくか、規則性を見いだすことで、未来を予測する知識を得ます。
私たちは、その規則性を、図に描いて理解することができます。ちょうど、電車の時刻表を想像してください。たくさんの電車が、いつ何処にいるか、はっきりわかりますね。
時刻表は、表だけれども、これをグラフにすると、電車の位置を視覚的にとらえることができます。電車の位置を、空間方向と時間方向をそれぞれ軸としたグラフに書き込んでしまいます。
極端な話、時間と共に移り変わる全ての出来事は、一つの図形で理解することができるようになります。図形を扱うのは数学で言うところの幾何学です。とても大げさな表現をすると、「自然法則は幾何学の言葉で記述される」ということになります。
x-tグラフと点とイベント
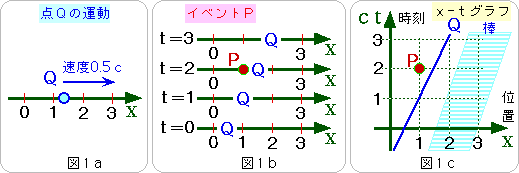
図1a をごらんください。xで代表される座標の上を、点Qが動いていきます。これを各時刻ごとに、下から上へ積み上げて描いてみましょう。すると、図1b のようになります。
これを連続的に表すためには、縦に順番につなげて、図1c のような、
ある場所で、ある瞬間に、Pと呼ばれるイベント(=出来事)が、おこったとしましょう。これは、
大きさを持った棒は、どのように書き込まれるかというと、図1c のように面としてあらわされます。ちょうど、新しいチョークを、黒板に横にしてくっつけて、擦ってできたような図形。棒の長さは、図1b のような状況で測ればよいので、図1c では、棒を表す面を、時刻一定の線で切った切り口の長さを求めます。
なお、このグラフ用紙の上に、コーヒーをこぼしてしまったとしましょう。
グラフ用紙は、水分を吸って、ところどころ伸びてしまいました。もうベコベコです。こういう状況を俗に「時空が歪んでいる」といいます。いくつかの、お互いに一定の間隔で直進しているハズの点の集まりが、膨らんだシミの部分を通り抜けると、おたがいに集まってしまいます。点をあらわす線は、それぞれまっすぐに引いてあるのに、です。これを使って、ものが落ちる性質「重力」を表現することができます。
さて、問題です。次の内容は、点ですか?それともイベントですか?
1、初代校長先生の銅像の鼻先。
2、タケシ君が手をたたいた。
別の座標を重ね書きしてみよう
x-tグラフの中に、新たに|
(ct’,x’)=(0,0) → (ct,x)=(0,0) (ct’,x’)=(1,0) → (ct,x)=(Cosh,Sinh) (ct’,x’)=(0,1) → (ct,x)=(Sinh,Cosh) ここに、 |
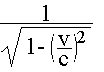 , Sinh =(v/c)Cosh
, Sinh =(v/c)Cosh
となります。例えば、速さvの値を光の速さcの60%だとすると、
|
(ct’,x’)=(0,0) → (ct,x)=(0,0) (ct’,x’)=(1,0) → (ct,x)=(1.25,0.75) (ct’,x’)=(0,1) → (ct,x)=(0.75,1.25) |
と、いうことになります。それぞれの点は、図2の様に表されます。
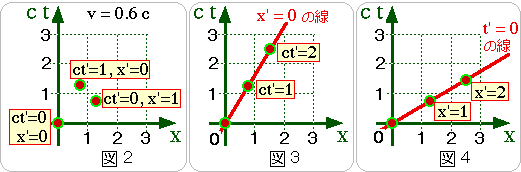
同様にして、
つぎに、原点
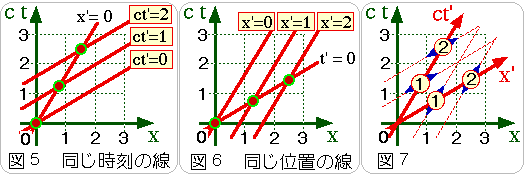
こうして、何本も線を引くと、図7のように、斜めにひしゃげた座標を書き込むことができます。これで、同じグラフ上の一つの点が、Oを基準とした世界での値と、O’を基準とした世界での値の、2通りの値に読みとれるようになります。
| 各自、図7の様な菱形の座標をグラフ用紙の上に作成してみてください。 |
お互いに時間が遅れる
1-3 で、時間の遅れについて扱いましたが、これが、お互いに遅れていることが、ローレンツ変換を使って理解できます。原点O’に対して固定された、1つの時計で「時間2」を測ったとします。これは、図8の様になります。時計は点Pから、点Qへと移動します。この間、O’に対して固定された座標x’の読みはゼロのままです。時間の読みは、斜めに傾いた線で読みとって2です。この間、原点Oに対して固定された座標では、時間をまっすぐ上向きに読みとるので、時間は 2.5 経過していることが読みとれます。
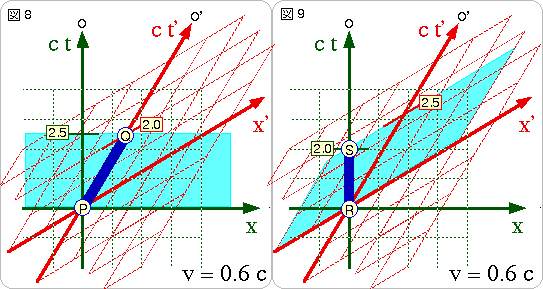
では、原点Oに対して固定された、1つの時計で「時間2」を測ったとします。これは、図9の様になります。時計は点Rから、点Sへと移動します。この間、Oに対して固定された座標xの読みはゼロのままです。この時間を、斜めに傾いた、原点O’に対して固定された座標の時間で読みとると、やはり、2.5 という答えが出てきます。
これを計算で導出すには、点Qの値を計算します。ローレンツ変換に、
| 問題1:一定の速度vで移動する宇宙船の中の時計が、T秒進みました。その間に、宇宙船の外の時計は、いかほどの時間を刻んでいますか?ローレンツ変換を用いて計算してください。 |
お互いに進行方向に縮む
1-3 で、長さの縮みについて扱いましたが、これが、お互いに縮んでいることが、ローレンツ変換を使って理解できます。時間の場合と同じ要領で考えます。
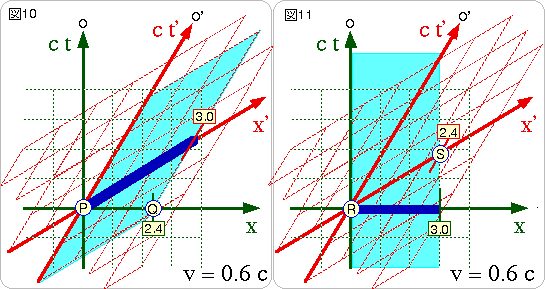
図10のマーク部分は、
図11のマーク部分は、Oに対して静止している長さ3の棒を表しています。
この長さは、Oから見て、同時刻に測らなければならないから、xの方向にxの目盛で測ります。これを
これを計算で求めるには、図10の場合、点Qについて計算してみます。ローレンツ変換に、
| 問題2:静止しているときに測った長さがLの棒があります。この棒が、長さ方向に、速さvで、移動していきました。棒の長さは、いくらになったでしょうか?ローレンツ変換を用いて、計算してください。 |
|
●時間の遅れ ●ローレンツ収縮 |
について知ることが出来ました。
2-5-2、超光速と棒とタイムマシン
超光速 ・・・?
ローレンツ変換を使った速度合成の式から、光より遅いどんな速さを足しても、光の速さを越えることができないことが、わかっています。しかし、遠い未来に、未知の物理法則が発見されて、光の速さを越えることができるようになったとしましょう。これをグラフに表してみましょう。たとえば、図1のイベントAとイベントBの間がそれに当たります。グラフは時間方向にc倍に引き延ばされているから、光の先端の位置は、軸から45゜の傾きを持った直線で表されます。AB間はその傾きよりも緩くなっていますので、同じ時間の間に、光よりも遠くに行けることを示しています。
点の動きを、体験してみましょう。まず、スリットを作ります。厚紙を2枚用意してください。厚紙のへりのまっすぐなところを、向かい合わせて、平らなところに置き、隙間が
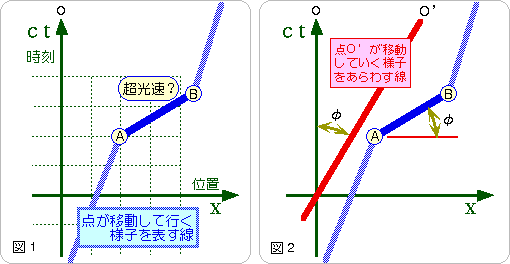
さて、この点(グラフ上では線)を、点
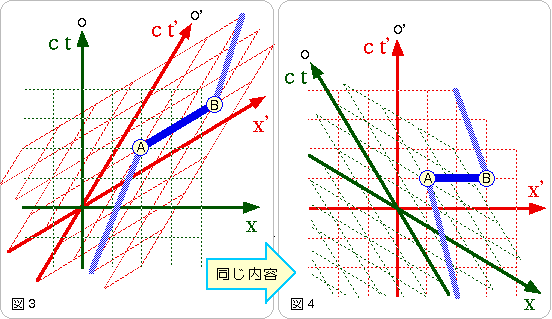
イベントAとイベントBは、同じ時刻にあらわれます。光の速さがOと
図3を
こうなると、線分ABは、「光の速さを越えた点の運動」と言うよりも、「棒」と呼んだ方が適切かもしれません。「時刻
では、棒と瞬間移動の違いは何でしょう?それは、移動の場合には、原因と結果の関係があるということです。イベントAのできごとが、イベントBに影響を与えているならば、AからBへ「移動した」ということができるでしょう。棒の場合には両端のできごとは、全く無関係に存在することができます。とりあえず、「瞬間移動装置」が作れたものとして、話を先に進めてみましょう。
タイムマシン ・・・?
瞬間移動装置を作ることができたならば、時間を、さかのぼることができます。瞬間移動装置の技術を応用して、タイムマシンが作れるでしょうか?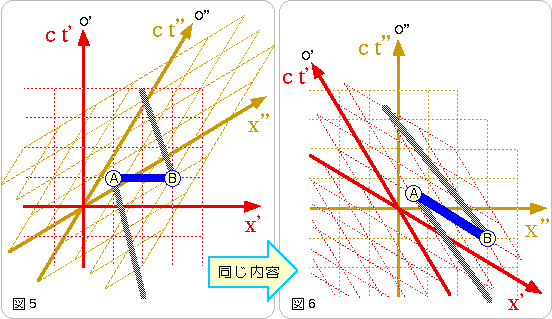
図5をご覧ください。イベントAに向かって
| では、ここで問題です。この瞬間移動装置A→Bが、世界中でたった1個だけあったとして、過去の自分に会うことができますか?考えてみてください。 |
問題の答えへの大ヒント:
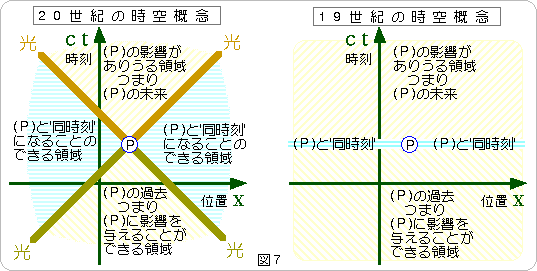
図7をご覧ください。19世紀までは、時間の概念は単純でした。しかし、今日では、ローレンツやアインシュタインによって、同時刻というのは相対的な概念であることが明らかにされています。
イベントPに向かう光と、イベントPから発生した光を、グラフに書き込みます。この45゜の線の左右両側に存在するイベントは、どれでも適当なローレンツ変換をすることで、必ず、Pと同時刻になるように、座標系を選ぶことができます。つまり、この領域は、イベントPと同時刻になりることができるイベントの集まりです。従って、この領域でおこった出来事が、イベントPに影響を及ぼすことは、できません。
45゜の線を挟んで上下には、Pの未来と過去が広がります。未来側は、イベントPの影響を受けることのできるイベントの集まりです。過去側は、イベントPに影響を与えることのできるイベントの集まりです。ただし、ここには、ルール違反の「瞬間移動装置」や、「タイムマシン」が、一つも存在しないことを、前提としています。
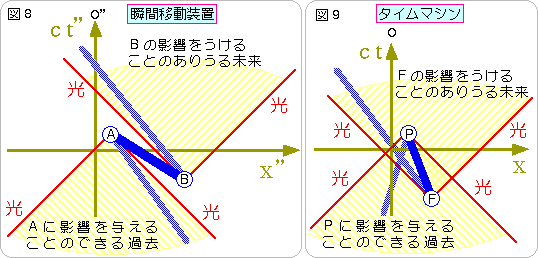
図8をご覧ください。どんなにローレンツ変換を繰り返しても、AとBを結ぶ線の傾きを45゜より深くすることはできません。過去の自分に会うためには、図9のように、点が描く線が交わらなければなりません。しかし、瞬間移動装置では、図8のように、BがAの過去に入ることができません。したがって、瞬間移動装置1機のみを使って、過去の自分に会うことはできません。
では、もし、タイムマシンを作ることに成功したとして、過去の自分を殺してしまったら、どうなるでしょうか・・・?(文献2,3)この問題は、ずっと後で取り扱います。
