1-3、走っても光の速さが変わらないなら・・・
正確な実験結果から、光の速さは、光源と測る人がどんな速さで移動していても、変わらないことが、わかりましたが、このことから、今度は奇妙な結論が導かれます。速さは（道のり）／（時間）なので、距離又は時間の測り方に修正が必要になるのでした。
- 時刻を測るときに、測られるものと、時計が同じ場所になければならないのですが、これが離れている場合は、何らかの信号をやり取りして得られた結果から時刻を算出しなければなりません。信号として光を採用してもよいわけで、光の速さが定数であることから、走っている時計はゆっくり時を刻むという結果が出ます。
- 動いているもの長さを測るとき、始点と終点を同時刻に測らなければならないのですが、光の速さが定数であることから、この「同時刻」という考え方に修正が必要になり、棒が進行方向に縮むという結果が出ます。
- また、これらにともなって、走っている物体は外から受けた衝撃による加速がにぶくなり、つまり質量が増えることになります。
これらはとても奇妙に感じられるかもしれませんが、光の速さに近い速度と言う極限の環境で顕著になってくるので、私たちの日常生活で経験できる内容とはかけ離れてしまっています。宇宙論や素粒子物理学などに日頃から接して、光の速さが身近に感じられる人たちにとっては、むしろ当たり前の出来事です。
ここでは、時間や空間などのトピックスを手っ取り早く知りたい人たちのために、厳密な議論は抜きにしてこれらを説明いたします。多くの通俗書は、このレベルで終わっています。たったこれだけを引き延ばして本を出すんだから、いい商売だね。
1-3-1、走ると歳をとらない！？
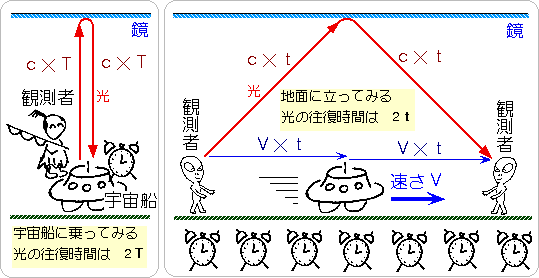
地表近くを高速で移動する宇宙船を考えます。宇宙船の進行方向と平行に鏡を置きます。 宇宙船から、光を出して、その鏡で反射させて、もとの場所へ戻って来るまでの時間を測ります。 宇宙船に乗っている浦島氏と、地面の上にいる観測者には、まったく同じ時計が渡してあります。 また、地面には、その同じ時計を多数、隙間なく置いておきます。 これらの時計は狂いもなく、はじめから正確に時刻を合わせてあるものとします。 地上の時計は、離れた同士でも、隣同士の時刻がきちんと合っているので、正確に合っていることが判ります。
- 宇宙船の浦島氏が測ったところによると、光が地面 との間を往復する時間は、「２Ｔ」 でした。
- 地上の観測者が測ったところによると、 光が宇宙船との間を往復する時間は、「２ｔ」 でした。
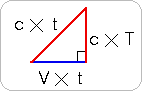
図の四角枠の中をご覧ください。光の速さは光源や観測者の速度に依らずに一定値（c = 299792458m/s）でしたから、どうしても、Ｔよりｔのほうが長くなってしまいます。 つまり宇宙船の中の浦島氏にとっては少ししか時間が経っていなくても、 地面の上では、長い月日が流れてしまったということがありえます。 地上の観測者から見れば浦島氏の時間の流れがゆっくりになっているように見えるでしょう。一体どうしてしまったのでしょう？ 図の三角形は、直角三角形ですから「ピタゴラスの定理」を使って計算すると、
( c×T )2 = ( c×t )2 − ( V×t )2
となっています。 （この式の左辺は浦島氏が測定できる量、右辺は地上の観測者が測定できる量でまとめてあります。なお、浦島氏にとっては、自分がどんな速さで動いているのかを知る方法は、ありません。）
この時間の遅れは、様々な実験でも、よく確かめられています。 理論で奇妙な結果が出てきたら、理屈をこねまわすよりも、実験してみることがが有効です。
証拠その１：寿命が延びる！
光の速さに近い速さまで物体を加速するには、その物体が軽い方が容易です。 物体を小さく小さくしていくと、やがてこれ以上分解できない「素粒子」に行き着きます。 たいていの素粒子は、寂しく独りにしておくと、勝手に壊れてしまいます。 つまり、寿命があります。この、寿命が延びたことを観察すればよいです。 光の速さに近づくような素粒子の実験は、数多く行われていますが、 その寿命が、期待通りに伸びていることが、現実に観測されています。 実験装置もこの理論をもとに設計されていますが、この寿命に関してなんら障害はありません。
初めにこの事をはっきりさせたのは、μ粒子と呼ばれる素粒子です。（文献１） これは、宇宙の強力な放射能が、高いところの地球大気の原子と衝突して生まれるのですが、 壊れてしまうまでの寿命が、およそ0.0000022秒しかありません。 つまり、たとえ光の速さで、地上へ向かったとしても、寿命が変わらなければ、 660ｍしか進めません。 地上に降ってくる前に、壊れて無くなってしまうはずです。 しかしながら、この粒子が地上で観測されています。 これは、粒子が経験する地上までの時間の長さが、 地上で測る時間の長さよりも、とても短いことを意味しています。
証拠その２：飛行機に時計を乗せて測ってみたら、ほんとにそうだった！
ジェット機に、とても正確な、セシウム原子時計を４個も積んで、 地球を一周してみたら、本当に時間が遅れていることが確かめられています（文献２）。 たかだか毎時1000km 程度の速さのジェット機でも、 ちゃんと（0.0001秒程度の）時間の遅れが観測できます。 西回りと東回りと地上の時計の針の進み方は、それぞれ異なります。 太陽を追いかけて飛ぶ西回りの飛行機の針が一番良く回り、 次に地上の時計、東回りに飛んだ飛行機の針が一番回りません。 なぜでしょう？
ヒント：基準となる時計を、どこか、地球の自転の影響を受けないところに置いてみます。
ところで、動いている宇宙船と止まっている地面の立場をひっくり返して見ると、 おかしな事に気が付きます。 宇宙船の浦島氏の立場から見れば、地上の観測者の方が動いていくのですから、 今度は、地上の時計の方が、ゆっくりになってしまうのではないのでしょうか。 つまり、お互いに相手の動きがゆっくりになっているという事になります。 いったい何が地上と宇宙船とで違っているのでしょうか？ じつはどこもおかしくはなく、矛盾でも何でもありません。 なぜでしょう？ひとまずは、よく考えてみてください。 答えは「2-3、ローレンツ変換」の項目で。
1-3-2、目的地が近くなる
光の速さがどこから見ても一定であるという事実から、またまた不思議な現象が現れます。 速さと時間を掛けると道のりになりましたから、２点間の距離にも影響が出てきます。 じつは、光に近い速さで走ると、目的地が近くなってしまいます。別の見方をすると、 硬くて縮まない棒を、棒の方向に光に近い速さで走らせると、縮んでしまいます。 これはアイルランドのフィツジラルド ( George Francis Fitzgerald 1851-1901 ) が考え出して、 オランダのローレンツ ( Hendrik Antoon Lorentz 1853-1928 )が理論を完成（1892年に発表）させたので、 「ローレンツ・フィッツジラルド収縮」と呼ばれています。 文献によっては単に「ローレンツ収縮」と書かれているものも多いです。 「アインシュタイン収縮」とはいいません。 アインシュタインが、1905年に相対性理論の論文を発表するよりも、 ずっと前から知られていたことだからです。
どれほど縮むものか、計算してみましょう。
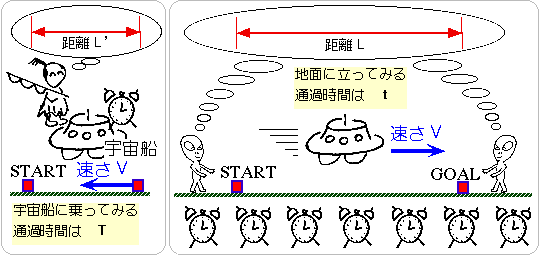
一定の距離に固定された、２点を用意します。宇宙船が一定の速度で、START地点を通過して、GOAL地点に到着するまでの時間と距離を測ります。地上から宇宙船の速さをＶとすると、宇宙船から見た、START地点と、GOAL地点の速さも、やはりＶとなります。宇宙船から見て、START地点からGOAL地点に至るまでの時間をＴ、距離をＬ’とします。地上から見て、宇宙船がSTART地点からGOAL地点に至るまでの時間をｔ、距離をＬとします。速さは、道のりを時間で割ったものだから、時間は、距離を速さで割ったものとなります。従って、宇宙船で計った時間と、地上で計った時間をそれぞれ比べると、
たん宇宙船から測定した値の間の関係 ： Ｔ＝Ｌ’÷Ｖ
地上から測定した値の間の関係 ： ｔ＝Ｌ ÷Ｖ
が、成り立ちます。前節の結果から、 宇宙船の浦島氏の体験する時間の進み方と、地上の観測者の時間の進み方の間には、
( c×T )2 = ( c×t )2 − ( V×t )2
という関係がありましたから、Ｔとｔをそれぞれ代入して、両辺に(Ｖ/c)２を掛けてルートすると、
Ｌ’= Ｌ×
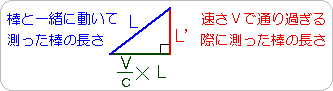
といった関係式が得られます。 右辺は１よりも小さな数を掛けているので、Ｌ’はＬ よりも小さな値となってしまいます。 START地点からGOAL地点にかけて、まっすぐな棒を指し渡すと、Ｌ’とＬ は棒の長さを表します。Ｌは、地上で測った長さだから、棒を静止させて測った長さです。Ｌ’は、宇宙船から測った棒の長さだから、速さＶで走り去る棒の長さを意味しています。
これらの長さの関係を直角三角形の辺の長さで表すと、左の図のようになります。 たとえば、宇宙船の速さが光の速さの80％だとすると、Ｌ’は Ｌ の 0.6 倍まで縮みます。 日常生活の経験では、Ｌ とＬ’は等しくならなければならないものですが、 これらを等しいとすると、こんどは話のつじつまが合わなくなってしまいます。
ところで、宇宙船と地上の立場をひっくり返してみると、 地上の方が動いているわけですから、 こんどは、Ｌ’よりもＬ の方が短くなるのではないのでしょうか？ つまり、「お互いに縮んでいる」のです。 これは、どこもおかしくはなく、矛盾でも何でもありません。 どういうことなのかよく考えてみてください。 ２人の観測者の立場の違いについてよく注意してみるとわかります。 答えは「2-3、ローレンツ変換」の項目で。
1-3-3、進行方向と垂直な方向にはやっぱり縮まない
図のように、同じ半径の、全く同じ輪を、同じ速さで正面衝突させたとします。
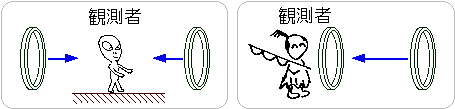
どちらかが縮んでいれば、輪はぶつからずに、すり抜けるはずですが、 両方の輪で条件が全く変わらないので、輪はぶつかります。 一方、片方の輪といっしょに動いてみると、もう一方の輪が近づいてくるのが見えます。 もし、この輪が縮んだり、伸びたりしていたら、ぶつからずにすり抜けて行くはずです。 しかし、ぶつかることが、わかっているのですから、伸びたり縮んだりしていません。 つまり、運動方向と垂直には、変形しない物体は、やっぱり、伸びも縮みもしません。 実は1-3-1で、時間の遅れを導くときに、この事実を使っています。
1-3-4、質量が大きくなったように見える
ニュートン ( Sir Isaac Newton 1643-1727 イギリスの物理学者）が確立した力学によると、 運動の変化のしにくさを表しているのが質量(= mass)でした。 エアーホッケーのコマをはじいて衝撃を与えた場合を想像してみてください。 コマの質量（直感的には「重さ」）が大きいほど、手応えが大きくなります。 つまり、質量が大きなほど加える衝撃を大きくする必要があることがわかります。 また、加えた衝撃が、大きければ大きいほど、速度の変化は大きくなります。 このコマに加えられた衝撃の大きさに対応する物理量を「力積(= Impulse)」と呼ぶことにします。 力積は、衝撃を加えられた物体の「質量」と「速度の変化」に両方比例し、他に関係する量が無いから、 これらの積と等しくなるものとします。式で書くと、
[(質量)×(速度)]衝突後−[(質量)×(速度)]衝突前＝（外から加えられた力積）
一方、この節の始めで述べたように、光に近い速さで移動する乗り物の中でおこる出来事は、 「ゆっくり」進行しているように見えます。 このため、外部から何らかの衝撃があった場合の反応も緩慢になります。 つまり、速度の変化が小さくなるということです。 同じ力積でも、速度の変化が小さいほど、質量は大きい事になりますから、 光に近い速さで移動する物体は、質量が増えたかのように見えることになります。
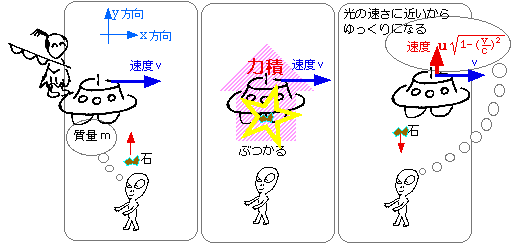
どのぐらい質量が増加するか計算してみましょう。いま、無重力の宇宙空間で、観測者に対して静止している宇宙船めがけて石をぶつけたとします。石の衝突の衝撃で、宇宙船は、ｙ方向に小さな速さｕで動き出したとします。このときの宇宙船の質量をｍo とすると、小石が宇宙船に与えた力積は、掛け算して、（ｍo×ｕ）となります。
今度は、同じ宇宙船が、ｘ方向（ｙ方向と垂直）に、速さｖで移動しているとします。これに、先ほどと全く同じ条件で石をぶつけてみたとしましょう。ｘ方向に宇宙船と共に移動する人にとっては、先ほどと同じことがおこるわけですから、ｙ方向に速さｕで宇宙船は動き出します、しかし、石を投げた側からすると、その動きは倍に遅くなっています（ｃは光の速さ）。
例えば、すれ違う速さ v が光の速さの 60% の大きさだとすると、宇宙船の中の時間は(1-3-1)で述べたように 1.25 (= 1/) 倍に引き延ばされて見えます。速さは長さ割る時間で、運動方向と垂直な方向の長さは動いていないときと変わらないことがわかっているから、分母の時間だけが修正されて、衝撃で生じた宇宙船の速さは u の 0.8 (= 1/1.25 ) 倍に遅くなるわけです。
このときの宇宙船の実効的な質量をｍとすると、加えられた力積が先ほどと同じ（←論理の飛躍がありますが、端折ります）ことから、
ｍ×｛ｕ×｝＝ (力積) ＝ｍo×ｕ
両辺を整理して、速さｖで移動する宇宙船の実効的な質量ｍは、静止している時の質量ｍo を用いて、
ｍ＝ｍo÷
と、書かれます。特にｍの事を「運動質量」、ｍo の事を「静止質量(= rest mass)」又は「固有質量(= proper mass)」と呼ぶ人もいます。単に粒子や物体の「質量」といった場合は、秤に対して物体を止めて測った質量であるｍo の方を指します。
光の速さを基準にして測った速さを横軸に、静止質量ｍo＝１の物体の運動質量を縦軸にグラフを書くと、次のようになります。
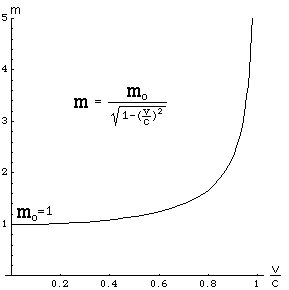
これは、速さが光の速さに近づくに従って、爆発的に慣性が増すことを意味しています。光の速さに近づくに従って、どんなに大きな力で押しても、ほとんど加速せず、運動質量ばかりが増えていくことを意味しています。
なお、運動質量について、アインシュタインが初めに公表した論文では、運動方向に対して垂直方向からの力積と、平行な方向からの力積に対して、値が異なっていました。しかし、その後の研究で、同じとして良いことがわかりました。
まとめ
光の速さ近くで移動する物体について- 内部の動きはゆっくりに見える：どんな証拠がありましたか？
- 進行方向に縮んで見える：長さ10cmの鉛筆に、モノサシをあてがって、一緒に、光の速さの80%の速さで運動させたら、鉛筆の長さの読みは何cmですか？
- 進行方向と垂直には縮まない
- 質量が増えて見える：次のコトバを説明してください→「力積」「質量」
