1-5、光と質量

※この章はむずかしいので、物理IIを履修していない人は飛ばしてください。
　この章では、エネルギーと質量の等価性について述べます。 つまり、エネルギー保存則を考えるときには、 その物体の質量も、エネルギーに加えないと保存しないという性質です。 式を使って象徴的に書くと、

E = mc²

となります。ここで、E はエネルギー、m は質量、c は光の速さです。 この式は、アインシュタインの名声と共に有名になりました。

一般には、この関係式が、核兵器の開発を理論的に裏付けるの原理として重要であったと、思われています。 しかし、これは通常の化学反応でも起こっていることでありまして、 原子力エネルギーを取り出すためだけの理論というわけではありません。 ただ、化学反応などの場合には、ｃの大きさがとても大きいために、 質量の変化が小さすぎて、測ることができないのでした。 つまり、アインシュタインの理論が、核兵器開発の原点になったという考えは誤りです。

実は、この関係式は、物質に対する光の吸収と放出に関して云えば、 アインシュタインの理論を使わなくても、 つまり、「相対性」をあからさまに強調しなくても、 「マクスウェルの方程式」だけから導出できます。 この方程式は、19世紀にマクスウェルが、複雑きわまりなかった、 電気と磁気の法則を、数学の力を借りて、簡潔にまとめあげたものです。

話の筋道としては、電磁波のエネルギーＥと運動量Ｐの間に、

Ｅ = ｃ｜Ｐ｜

の関係があることが、マクスウェルの方程式（電気と磁気の法則）から導けます。 これを使って、光ではない、一般の物体が、光を吸収または放出したときに、 E = mc² の関係があることを導くことができます。 電気と磁気の法則の話は、ここでは触れずに、問題の核心へと進みましょう。

1-5-1、光を吸収した物体の質量は増える

アインシュタイン自身が、1946年に発表した、わかりやすい導出法を紹介します（文献１）。 この方法は、以下の３つの法則だけを使います。
　１、運動量保存の法則
　　　　・運動量（ベクトル）の総和は合体／分裂の前後で変わらない
　　　　・物体の運動量の大きさは、( 物体の質量 )×( 速さ)
　２、光（＝電磁波；論文では「輻射の複合体」）の運動量の式
　　　　・光の運動量の大きさは、(光のエネルギー)／( 光の速さ )
　３、光行差の式
　　　　・自分が走ってみると光の進む向きが変わって見える
　　　　　→1-1-3「ブラドレー」参照

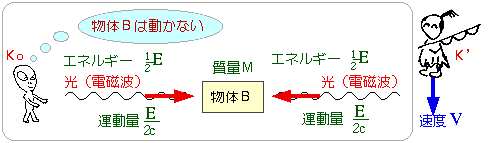
外部から力を受けていない、質量Ｍの物体Ｂを考えます。 これを、物体Ｂに対して静止している観測者Ｋo がいます。 物体Ｂの両側から、左右対称に光を照射します。 左右から来た光の道筋が一直線になるように、まっすぐ照射します。 前後左右に対称ですから、物体は動きません。 一方の光のエネルギーを、Ｅ／2 とすると、 光が吸収されたあとの物体Ｂのエネルギーは、Ｅです。 具体的には、熱などの形で存在するでしょう。
　これを、ｚ軸方向負の向きに、一定の速さｖで、ゆっくり移動する観測者Ｋ’が見るとどうなるでしょうか？ Ｋo からみて、物体Ｂは光の吸収前後で静止したままなので、 観測者Ｋ’からみたら、物体Ｂは、速度を変えずに走り続けます。

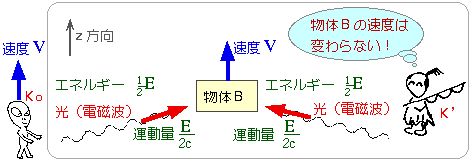
ところが、光（＝電磁波）は、そのエネルギーを、光の速さで割った値の運動量をもっていますから、 光の運動量のｚ方向成分が存在します。 運動量保存則は必ず成り立ちますから、物体Ｂが光を吸収した後には、 光の運動量の分だけ、物体Ｂのｚ方向の運動量が増加します。 つまり、光を吸収したことによって、速度が変わらずに運動量が増加するという状況になります。 これは、質量が増加する以外に、矛盾のない理論を進めることができないことを意味しています。

では、質量の増加分を勘定してみましょう。 図より、観測者Ｋ’から見た光の運動量は、左右合わせて ( Ｅ Ｖ／c² ) です。 光を吸収した後の物体Ｂの質量をＭ’とすると、運動量保存則より、次の式が成り立ちます。

Ｍ’Ｖ ＝ Ｍ Ｖ＋ ( Ｅ Ｖ／c² )

すなわち、物体Ｂの質量の増加分は、光のエネルギーをｃ^２で割ったものになっています。

（質量の増加分） ≡ Ｍ’ーＭ ＝ Ｅ／c²

以上より、物体が光を吸収すると、そのエネルギーに比例して、 質量が増加することが示されました。
　吸収された光は、物体の中で、光のままの形で存在しているわけではありません。 おそらくは、光は消滅して、そのエネルギーは、 物体内部の熱エネルギーなどに変わっていることでしょう。 すると今度は、熱を持った物体の質量は増加するという話にもなります。 つまり、質量の増加の本質はエネルギーです。 エネルギーは様々な存在の仕方の間を、移り変わるから、 上記の関係式は、光に限らず、一般に成り立つものだということが、考えられます。 つまり、エネルギー保存則と、質量保存則は、別々に考えることができなくなり、 以下のように書き換えられなければなりません。

Σ_全て（エネルギー）＋Σ_全て（質量）×c²＝（一定の値）

1-5-2、光子の質量

光には、粒子のようにカタマリとして振る舞う性質も在りまして、その粒子としてみた光のことを、「光子」（コウシと読む。英語では Photon）と呼んでいます。光子の質量はいかほどのものなのでしょうか？
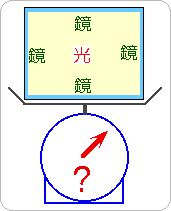
　答えを先に申しますと、光の進行を止めようとすると、速度が遅くなる代わりに、 振動数が減少していき、最後には、光自体が消滅してしまいます。 このことから、光子の質量はゼロです。 しかし、鏡張りの箱の中に、光を閉じこめて、質量の差を求めると、

( 光のエネルギーＥ ) ＝ ( 質量の増加分△m )×( 光の速さc )^２

の関係が導かれます。

1-5-2-1、光は止められるか？

光を止めて、重さを量ることはできるでしょうか？ 結論を先に申しますと、ノーです。 光の速さは、どこから見ても一定の値ｃをとりますから、止めることが、できません。 では、止めようとすると、どの様なことがおこるのでしょうか？

光について考える準備として、飛んできたボールを止める方法を考えましょう。 通常は、グローブなどで、簡単に受けとめて、止めることができます。 しかし、これは、ボールとグローブの摩擦を利用しています。 キャッチボールを続けていると、グローブが熱くなってきた経験はありませんか？ これは摩擦によって熱が発生したからです。 光の場合について当てはめてみると、熱の発生を許すとするならば、 光が物質に吸収されてしまった場合に相当するでしょう。 このケースは、前の章で扱いました。 しかし、「光を止めようとすると、どうなるのか」という問いには答えていません。

では、熱を発生させずに、ボールを止める方法はないのでしょうか？ あります。ボールから逃げていく壁にぶつければいいのです。 壁とボールは完全弾性衝突をするものとします。 別のコトバで言い換えると、壁から見たボールの速さは、向かってくるときと、 跳ね返って遠ざかるときで、同じになるものとします。 そして、壁の質量はボールと比べて大変大きく、 衝突に伴う壁の速度の変化は無視できるものとします。 すると、壁の速さをボールの速さの半分に選べば、ボールが止まることが示せます。

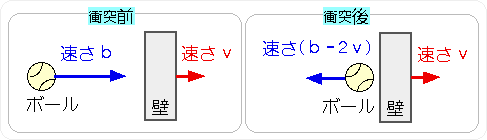
これを、光について当てはめてみましょう。 振動数ｆの光が、壁に向かっていくとします。 壁にぶつかった後の振動数は、壁が逃げているから、ドップラー効果によって、 振動数は、もとの値の (ｃ-ｖ)／(ｃ+ｖ) 倍にまで、減少します。 つまり、光は速さを変えることができないので、代わりに振動数が変化します。 光を止めようとすると、振動数がゼロに近づき、その存在自体が、消えてしまいます。 つまり、光を止めて測った光の質量の値はゼロです。

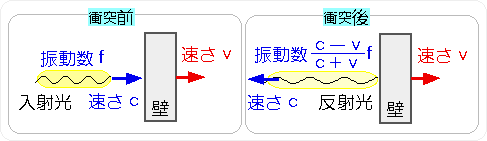
なお、光の粒子としての性質を捉えた「光子」のエネルギーは

（光子１粒のエネルギーＥ）＝（プランク定数ｈ）×（光の振動数ｆ）

ですから、光を止めようとすると、どんどん振動数が低くなっていき、 光子１粒あたりのエネルギーが、減少していきます。

1-5-2-2、光は　Ｅ＝ｃ|Ｐ|

( 光のエネルギーＥ ) ＝ ( 光の速さc )×( 光の運動量の大きさＰ )

という関係式は、純粋に、19世紀のマクスウェルの電磁気学の理論だけから導出できます。 しかし、それを理解するためには、高校で習う電磁気の法則を、 ひととおり理解しておかねばならず、道のりは遠いものとなってしまいます。 そこで、一計を案じます。もし、光の粒としてのエネルギーが振動数に比例することを、 認めていただけるならば、簡単な力学の法則から、光のエネルギーが、 光の運動量と光の速さの積と等しくなることを示せます。

（光子１粒のエネルギーＥ）＝（プランク定数ｈ）×（光の振動数ｆ）

振動数ｆの光子ひとつぶが、速さｖで走り去る壁にぶつかるとします。 反射した光子の振動数は、ドップラー効果により、｛(ｃ-ｖ)／(ｃ+ｖ)｝倍に、 小さくなります。壁の速度が、光子の衝突により、かすかに変化しますが、 無視できるものとします。この振動数の減少によって、光子のエネルギーは減少しますが、 この減少分は、仕事として壁に与えられたと考えます。 すなわち、

ｈ（ｆ-ｆ’）＝Ｅ−Ｅ’＝Ｋ’−Ｋ＝（壁に与えられた仕事）

仕事は力と変位の積で、また、壁の運動量の変化△ｐ＝ｐ’-ｐは、 ニュートンの運動方程式（力積の式ともいう　ｐ’-ｐ＝Ｆ△ｔ）により、 壁に加えられた力に時間を掛けたものだから、 壁に与えられた仕事は、速さと壁の運動量の変化の積となります。つまり、

　（壁に与えられた仕事）＝（　力　Ｆ　）・（変位△ｘ）
　　　　　　　　　　　　＝（△ｐ／△ｔ）・△ｘ
　　　　　　　　　　　　＝（△ｘ／△ｔ）・△ｐ
　　　　　　　　　　　　＝　　　ｖ　　　・△ｐ

以上を組み合わせると、ｈ（ｆ-ｆ’）＝ｖ△ｐ　となります。 この計算は少々正確さを欠いているように見えますが、微分と積分を用いて計算すると、 きちんと狂いなく正しいことが示せます。

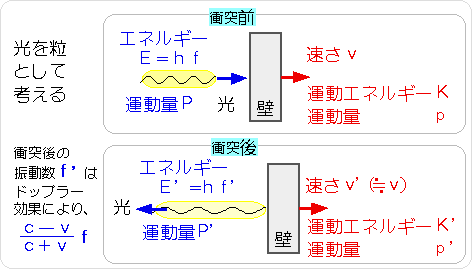
いっぽう、衝突前の光子の運動量の大きさをＰ、衝突後のそれをＰ’、とすると、 運動量保存則により、壁の運動量ｐｐ’との間に、以下の関係式が成り立ちます。 （光の進行方向が反転するので、逆向きを表すために、 Ｐ’には負号が付けられることに注意してください。）

（Ｐ）＋ｐ＝（─Ｐ’）＋ｐ’ 故に、△ｐ＝Ｐ＋Ｐ’ 以上より、△ｐを消去して、 ｈ（ｆ-ｆ’）＝ｖ・（Ｐ＋Ｐ’） を得ました。さらに、ドップラー効果の式から、 （ｆ-ｆ’）＝（ｖ／ｃ）×（ｆ+ｆ’） となるので、ｖを消去できて、 Ｅ＋Ｅ’＝ｈ（ｆ＋ｆ’）＝ｃ（Ｐ＋Ｐ’） となります。壁の速さｖを、ｃと比べて、とても小さな値とすると、 ＥとＥ’、ＰとＰ’の差は無視できるほど小さくなります。 よって、両辺を２で割って、 Ｅ＝ｃＰ が、得られます。高校の教科書でよく見かける形に書き直すと、 Ｐ＝ｈｆ／ｃ です。（ｆの代わりに、ギリシャ文字の「ν」が、よく用いられます。） 注意：「質量ｍ、速さｖの物体」の場合とは、違う式であることに気を付けてください。 Ｅ＝1/2 ｍｖ^２、Ｐ＝ｍｖ であるとすると、 Ｅ＝1/2 ｖＰ となり、（1/2）が付きます。

では、どうして、静止できる物体と、光の場合で、このような違いができたのでしょう？ 「光は、どこから見ても速さが一定の値ｃになる」という現象が本質です。 このため、壁にぶつかっても、速さが変わらないので、止まれないし、（1/2）が付かないのです。

1-5-2-3、閉じこめられた光の質量

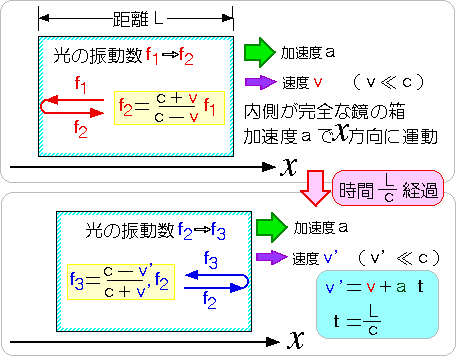
　内側が鏡張りの箱を考えます。もし、この鏡が、光を完全に反射するならば、 この箱の中に、光を閉じこめることができるでしょう。 光は永久に反射し続けて、しかも、外に出られないからです。 ここでは、この光の存在によって箱の質量が増えることを示します。 この運動をさせるために、外から加えなければならない力を計算すれば、 ニュートンの運動方程式から、箱の質量が求まります。 簡単のために、箱の形は直方体。一つの辺に沿って、ｘ軸を定め、 ｘ軸方向に、等加速度運動をさせます。その加速度の大きさを「ａ」とします。 光は、実際には、あらゆる方向に向かって走りますが、話しを簡単にするために、 ｘ軸方向だけに、進む場合を仮定します。 勿論、この仮定が無くても、結論に変わりはありません。

ある時刻で、振動数ｆ_１の光子が箱の後ろの壁にぶつかったとします。 そのときの、鏡の箱の速さがｖだとすると、ドップラー効果によって、反射した光子の振動数は、 ｆ₂=｛(ｃ+ｖ)／(ｃ-ｖ)｝ｆ_１ となります。箱の長さをＬとすると、 それから時間（Ｌ／ｃ）が経過したときに、光子は、今度は、前方の壁にぶつかります。 実は、多少経路が延びるために、時間がかすかに長くなりますが、 ｖはｃに比べて充分小さいものと考え、無視します。 光子が振動数ｆ₂で、箱の前方にぶつかると、 反射した光子の振動数は、ドップラー効果によって振動数ｆ₃へと、減少します。 このとき、箱は、加速度の影響で、先程とは速度が変わってしまっています。 その値をｖ’とすると、ｆ₃の値は、 ｆ₃=｛(ｃ-ｖ’)／(ｃ+ｖ’)｝ｆ₂ ここに、等加速度運動の公式により、ｖ’は、 ｖ’＝　ｖ　＋　ａ（Ｌ／ｃ） によって、与えられます。 いっぽう、光子が後ろの壁に与えた力積を△Ｐ1、前の壁に与えた力積を△Ｐ3とします。 光子の運動量は、エネルギー（ｈｆ）をｃで割ったものだから、 それぞれの力積の値は、図のようになります。 光子がひとまわりする時間は、（２×Ｌ／ｃ）だから、 光子ひとつあたりにつき、外から加える力をＦiとすると、力と力積の関係から、 　　　Ｆi△ｔ＝（△Ｐ1ー△Ｐ3） ここに、△ｔ＝２×（Ｌ／ｃ）　 これをＦiについて簡単な式にします。あとは、ひたすら計算。 図に書いてある△Ｐ1、△Ｐ3の具体的な形を代入する。 すると、ｆ1とｆ3の引き算が現れます。 ドップラー効果の式から、ｆ1とｆ3をｆ2で表し、 ｆ2で表されたｆ1とｆ3を式の中に代入します。すると、 ｛(ｃーｖ)／(ｃ＋ｖ)｝ー｛(ｃーｖ’)／(ｃ＋ｖ’)｝ という引き算が現れますから、通分して分子を簡単にします。 分子に（ｖ’ーｖ）の項が現れるから、それは、 等加速度運動の公式によって、加速度と時間の積に書き直します。 分母については、ｖとｖ’がｃと比べてとても小さいことを利用して、以下の近似を用います。 １／((ｃ＋ｖ)(ｃ＋ｖ’))≒１／ｃ^２ すると、 Ｆi ＝｛ｈｆ2／ｃ^２｝×ａ となる。ｈｆ2は光子のエネルギーだから、全て足し加えて、 （箱に加えた力）＝Σ_{｛全ての光子 i について｝}Ｆi　　　　　　　
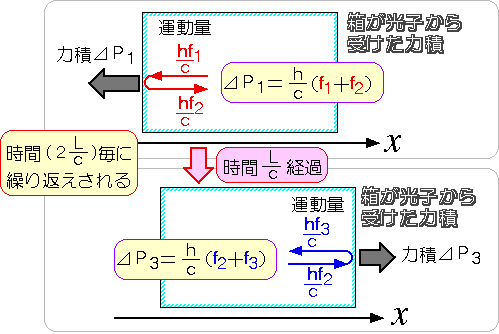
　　　　　　　　＝｛（全ての光子のエネルギーＥ）／ｃ^２｝×ａ よって、ニュートンの運動方程式によると、Ｆ＝ｍａだから、 箱の中の全部でエネルギーＥの光子の存在は、｛Ｅ／ｃ^２｝の分だけの、 質量を伴っていることが計算されました。 箱の外からは、中に光がつまっているかどうかは分かりませんが、 質量だけを測ることはできます。

　ここでは、箱の速度と光の進行方向が同じ場合について計算しましたが、 光が斜めに向かう場合についても計算できます。 その計算のコツは、ドップラー効果は使わずに、ブラドレーの光行差の式を使います。 つまり、箱の運動によって、光の進む向きが、ずれるために、運動量のｘ方向成分が、 箱の速度がない場合と比べて変化することを用います。 すみませんが、ここでは割愛させていただきます。