2-2、ガリレイとニュートンの相対性理論
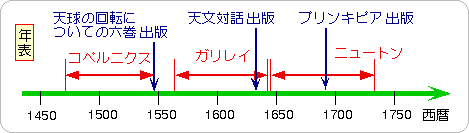
ガリレイ( Galileo Galilei 1564-1642：文献１）は、イタリアの科学者です。ピサの斜塔を使って、落下する物体についての実験を演じて見せた逸話は有名です。権威に盲従するのではなく、実際にやってみるところが、彼の素晴らしいところでしょう。そういう意味で、近代的な「科学」が、ガリレイから始まったともいえるのかもしれません。
ガリレイは、コペルニクス ( Nicolaus Copernicus 1473-1543 ポーランドの天文学者、医者 ：文献２）が唱えた地動説を支持したために、宗教裁判にかけられたことでも有名です。コペルニクスの主張はこうです：「地球は回っている。しかも回りながら太陽の回りも回っている。」 この話を聞いた当時の人たちは何を考えたでしょうか。お坊さんたちにとっては、神の創りたもうたこの大地が、クルクル回っているばかりか、太陽の周りを回っているなんていう話は、けしからん話だったのかもしれません。彼らはこう言ったことでしょう：「地面が動いていたら、汝らは振り飛ばされてしまうではないか！」 この問題点に対する説明が、1632年にガリレイが出版した著書「天文対話」（正式には Dialogospra i due`massimi del mondo Tolematico, e Copernicano =「世界の二大体系、すなわちプトレマイオスとコペルニクスの体系、についての対話」）で多く述べられているそうです。地球が、一定の速さで回っていても、その「速さ」を「感じる」ことは、できないということを本の中で説明しています。これは、のちに「ガリレイの相対性原理」と呼ばれるようになりました。「原理」というのは、最も基本的な事実ということです。これを、現在よく使われている言い回しで表現すると、こうなります。
| ＜ ガリレイ・ニュートンの相対性原理 ＞ |
|---|
| 慣性系 ( inertial system ) に対して、一定の速度で（回転せずに）直線運動をしている座標系 ( coordinate system ) もまた慣性系となり、全ての力学の法則は、この２つの座標系に対して、同じ形式で表される。 |
この２つの慣性系の間を関係づける式は「ガリレイ変換」と呼ばれています。初めて聞く人にとっては、まったくの呪文かもしれませんが、今のところは、それで結構です。慣性系とは、ある特別な条件を満たす座標系です。キーワードは、「慣性」「系」「座標」といったところでしょうか。これらについては、この章で、おいおい説明いたします。これは、通常、「ガリレイの相対性原理」と呼ばれていますが、「ニュートン」をくっつけたのは、ニュートンが提唱した力学の法則の言葉で記述されているからです。
ニュートン ( Sir Isaac Newton 1643-1727 ：文献３）はイギリスの物理学＆数学者です。ガリレイが亡くなった翌年に生まれています。大学の先生をしていましたが、晩年は、造幣局でニセ札の摘発に執念を燃やしています。彼の、有名な力学の法則は、1687年に刊行された、著書「プリンキピア」（正式には Philosophae naturalis principia mathematica =「自然哲学の数学的諸原理」）の中に、だいたい現れています。年表をご覧ください。人生の中程で主著を出せるのは、科学者として、幸せなことでしょう。
2-2-1、飛び出すな！車は急に止まれない
床を転がしたボールは、ころころ転がり、そのうち止まります。止まるまでの間、なぜ、転がり続けるのでしょうか？ 見えない何かが、押し続けているのでしょうか？
走っている車も、クラッチを踏んでエンジンから切り放しても、しばらく走り続けます。
なぜ、外から何もしていないのに、走り続けることが出来るのでしょうか？
さらに、月は、地球の回りを回り続けていますが、転がしたボールと違い、いつまで経っても動きが止まりません。なぜでしょう？ 昔のお坊さんたちは、「目には見えないが、天使が月を押し続けているからだ」とも考えたそうですが、本当でしょうか？
ここで、発想の転換をしてみます。もともとは
-
「何もしていないのに走り続けることが不思議で、
放っておけばそのうちに止まるということはあたりまえ。」
-
「何もしていないのに走り続けることはあたりまえで、
放っておけばそのうちに止まることが不思議だ。」
それに対して、転がしたボールが、そのうちに止まってしまうのは、止める方向に何かが働くからだと考えます。ちょうど、進行方向と逆向きに引っ張っているような感じです。こう考えると、ボールを押したときに加速する現象と、勝手に転がして減速する現象を、同じ仕組みで考えることが出来るようになります。またまた「共通性」を見つけだすことが出来ました。そこで、この、物体の速度を変化させる要因のことを、「力」と名付けます。これは、大きさと向きを持っていて、足し加えることが出来るように定義します。私たちが日常で体験するところの「力」とは、ことばの意味が微妙に異なるので注意してください。
地球の周りを回り続けている月が止まらないのはなぜでしょう。動き続けることが、当たり前で（慣性の法則）、止まるための力が働いていないからです。月の動きを止めないために、天使が押し続ける必要はないのです。ただし、本当に力が働いていないと、月はまっすぐ飛んでいって、地球から離れていってしまうはずです。実は、進行方向とほぼ垂直に、地球に向けて引っ張る力が働いています。ちょうど、ヒモの先にオモリを付けて、振り回しているような場合を想像してください。この、引っ張る力は、全ての物体と物体の間に働くので、万有引力と呼ばれています。
| ＜ ニュートンの運動の法則 ＞ | |
|---|---|
| 慣性の法則 | 全ての物体は、それになんらの力を加えない限り、いつまでも静止の状態、又は速度一定の等速直線運動を続ける。
（運動の第一法則とも呼ばれている） |
| 運動方程式 | (質量)×(加速度)＝(物体に加えられた力の総和)
（運動の第二法則とも呼ばれている） |
| （暗黙の 了解事項） | 力学系を２つの領域ＡとＢに分けたとき、ＡがＢから受ける力と、ＢがＡから受ける力とは、大きさが同じで、互いに反対の方向を向く。（「作用-反作用の法則」だとか「運動の第３法則」だとか呼ばれている） |
| 万有引力 の法則 | 宇宙にあるすべての質点は、他の質点を、それらを結ぶ直線の方向に、それれの質量の積に比例し、それらの間の距離の平方に比例するような大きさを持った力で引っ張る。 |
ところで「加速度」って何ですか？ これは単位時間当たりの、速度の変化のことです。たとえば、ある時刻に、物体の速度が
と、計算されます。ある瞬間の加速度を求めるためには、（計算上は）割る時間が短ければ、短いほど正確な値となります。つまり、２秒よりも、0.2秒。それよりも、0.02秒・・・の方が、正しい値に近づきます。
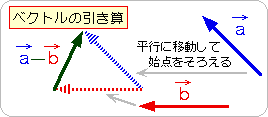
なお、速度の向きが変わる場合は、引き算をするときに、「ベクトルの引き算」が必要です。
ここでわたしたちは、ニュートン力学における重要な法則の一つ
- 慣性の法則
| 問題：慣性の法則が、成り立っていない世界を、想像してみてください。例えば、その世界で、まっすぐに一定の速さで走る電車の車内で、歩いたり、ボールを投げたり、お茶を飲んだりしている様子を、想像してみてください。どうなりますか？ みんなで話し合ってみましょう。 |
2-2-2、位置と時間の表現方法
ここでは、「座標」と、「座標系」について説明します。「ガリレイ変換」を理解するための準備です。数学が得意な人は、飛ばし読みしていただいても構いません。私の住所
位置をあらわすには、どのような表現ができるでしょうか？私はいま、どこにいるかと申しますと、広い宇宙の中で、地球の表面にいます。これで範囲は、かなり限定されます。そして、さらに絞り込んでいきます。地球の表面の中の、日本にいます。さらに日本を約30程の都道府県に区切った中のひとつ、北海道にいます。その北海道をさらに212の市町村に区切った中のひとつ、札幌市にいます。このように、大地を領域に区切って名前を付け、その中でさらに区切って名前を付けることを、くりかえすことによって、位置を正確に指定できるようになります。ただ、この方法の欠点は、地名と位置の関係をあらかじめ知っていなければなりません。地名を知らなくても何とかなる方法は、ないものでしょうか？
電車でＧｏ！
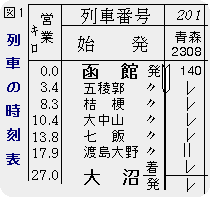話を簡単にするために、線路の上だけを動き回る列車について考えましょう。図１をご覧ください。青森を出た夜行列車は、函館に立ち寄り、五稜郭、桔梗・・・と駅をとばしていきます。列車の位置は駅名で表されます。「ただいま午前２時１分、列車は函館と五稜郭の間にいる。」という表現になります。
ここには駅名しか書いてありません。つまり、線の上の、とびとびの点にしか、名前が付けられていません。しかし、乗客にとては、乗り降りするのは駅に限られますから、駅名だけ知っていれば、充分です。
そして、運賃の計算には「営業キロ」が用いられます。この数字について、駅と駅の間で差を取り、運賃の計算の基準とします。ここで必要なのは、駅と駅の間の差の値だけです。駅以外のとろで、飛び降りた人の運賃は問題にしていません。（その人には、運賃ではなく、罰金が待っていることでしょう。）
座る標識
地名や、駅名や、日時など、場所や時刻に付けた目印のことを、座標といいます。座標は英語では coordinate（コーディネイト）です。図１や図２では、駅名が座標の役割を果たしています。「座」はその場所に固定して動かさないこと。「座ったら、てこでも動かない」といったイメージでしょうか。「銀座」と言ったら、お金がたくさんあるところといった気持ちでしょうか。「星座」といったら、お星様たちが、決まって現れる場所のことを意味するでしょう。
「標」は目印を意味します。「標識」といったら、その場所の地名や注意などが書かれていたりします。「商標」といったら、その商品に付けられた固有の名前を意味します。
場所に座標を割り振るときに、必ず守らなければならないルールがあります。
●場所の順番（位置関係）と座標の順番が、一致していること。
●場所と座標が、漏れなく対応していること。
順番を取り替えて、函館＞桔梗＞五稜郭＞大中山・・・などといった並べ方をしてはいけません。その順番で、電車がとまったら、乗客は怒るでしょう。また、図１の夜行列車は、渡島大野駅を通りません。渡島大野を通ると、遠回りをしてしまうので、線路を切り替えて別の近道を通るのです。従って、図１の駅名の並びは、七飯と大沼の間では、駅名の方が余ってしまい、座標としては適切でなくなってしまいます。渡島大野でいくら待っていても、この夜行列車は、通過しません。
便利な座標
線路と駅を、図に描いてみましょう。乗客の立場に立てば、図２のように、駅と駅の間を等間隔で描いても、なんら支障がありません。なぜなら、ここで重要なのは、駅を並べる順番と、駅と駅の間の距離の組み合わせだけだからです。乗客の立場で図に描くだけなので、実際の距離が図に反映されていなければならないといういわれはありません。函館から、１km 毎に目印を置くと、図２では、駅の間でまばらになったり、混み合ったりしています。（じつは、膨張する宇宙や、重力波の観測装置について考えるときに、この座標の発想は役に立ちます。）
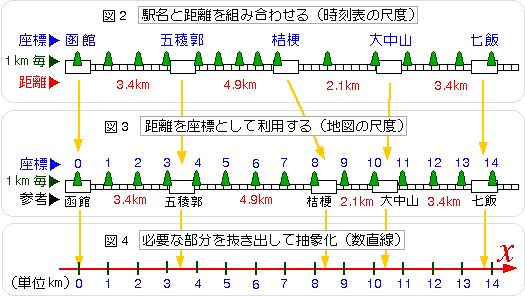
線路を工事する人たちの立場に立てば、どうでしょうか？枕木やレールを取り替えるには、線路の正確な寸法を、知らなければなりません。そのためには、座標の割り振りを、実際の長さに合わせた方が、便利でしょう。座標として、函館からの距離を使ってみましょう。これを絵に描くと、図３のようになります。１km 毎の目印は、等間隔になります。駅の間の距離は、実寸に比例し、地図と同じような描き方となります。地図と違う点は、曲がった線路をまっすぐに、伸ばして描いてあるところです。
さらに、この数字を使う方法の利点は、数字の桁を増やすことによって、いくらでも正確な場所の表現ができることです。「桔梗駅は、座標の値が8.3の所にある」→「桔梗駅の駅長室は、座標の値が8.36の所にある」→「桔梗駅の駅長室の机の上の灰皿は、座標の値が8.3612の所にある」といった具合に表現できます。（ところで、桔梗駅に駅長室が本当にあるかどうかは、私は知りません。）
以後、特にことわりのない限りは、この、距離を使った座標を採用することにします。じつは、曲がった空間や、歪んだ時空を扱う場合には、距離を使った座標を使えない場合が出てきます。話がそこまで来たら、図２のタイプの座標に戻ります。
ところで、図３から、具体的なものを全て取り払うと、なにが残るでしょうか？
図４のような、数直線になります。ここで、この線の上の「未知の点」の座標について考えてみます。「未知の」といっているので、具体的に数値を割り当てることができません。そこで、座標の値を、文字ｘであらわしておきます。その、「未知の点」の正体が、「実は桔梗駅だった」場合には、「
ゼロのむこうに
座標を割り振るための距離を、五稜郭から測ることにしたら、函館は、どうやってあらわせば良いでしょうか？
図５をご覧ください。ゼロの向こう側は、マイナスの数を使ってあらわします。新しい座標を使った函館の位置は、「−3.4」です。
玉ネギは、葉が層になっているそうだ
線路の上しか走らない電車の位置のあらわしかたは、わかりました。同様に、線の上の位置を座標で表現することができます。では、立体の場合については、どうしましょうか？ ヒントは玉ネギにあります。玉ネギの内部の点の位置を指定するとき、葉をむいていって、「外から３枚目に在った」という表現はできるはずです。ジャガイモの内部の点についても考えてみましょう。ポテトチップスを作る要領で、薄くスライスしていきます。切り始めから、数えて何枚目かという指定ができるでしょう。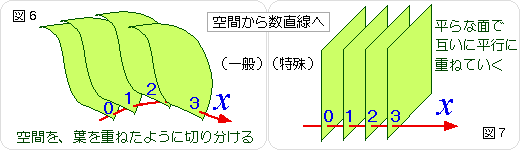
図６をご覧ください。左の図のように、曲面（葉）を用意します。これをすき間なく重ねていきます。次に、それぞれの葉を、ただ１回だけ貫くように、線を通し、この線に、先程の座標を割り振ります。すると、全ての葉にたいして、線上の座標の値を写し取ることができます。こうして、立体的な空間に対しても、座標の値を割り振ることができます。
しかし、このままでは、むずかしそうなので、設定をシンプルにします。図７をご覧ください。積み重ねる葉は、コピー用紙を重ねたように、まっ平らだとします。それらを千枚通しで穴を開けるように、数直線が垂直に貫きます。この数直線は、距離を使った座標値の割り振りを採用します。すると、葉と葉の間の座標の値の差が、距離によって与えられることになります。
以後、特にことわりのない限りは、この、平らな面に切り分ける座標を採用することにします。じつは、曲がった空間や、歪んだ時空を扱う場合には、この平らな座標を使えない場合が出てきます。話がそこまで来たら、図６のタイプの座標に戻ります。
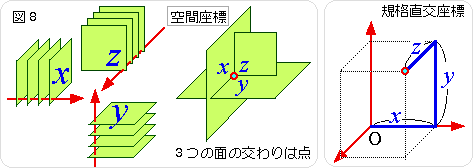
空間の中の点の位置を正確に定めるためには、図８のように、向きの異なる座標を３つ用意します。すると、点には３つの数の組（ｘ，ｙ，ｚ）を割り当てることができます。
時刻
時刻は時計で計ります。時計は、振り子や、水晶の発振や、原子から出る光などの自然物を利用して、時の刻みを定めています。この時計を支配している自然法則が、時計をどこに持っていっても変わらないという原理を前提として作られています。つまり、２つの時計を一緒に持ち歩いたときに、互いに異なる自然法則を応用した時計でも、時の刻みは同じになると、信じます。この原理は、当たり前だと思われるかもしれませんが、実は、すごいことなのです。時刻は、原則として、空間の座標の値のそれぞれに対して、与えます。そして、それらを合わせます。ことなる場所の時刻を合わせる方法は、大まかに、次の図のような２通りが考えられるでしょう。
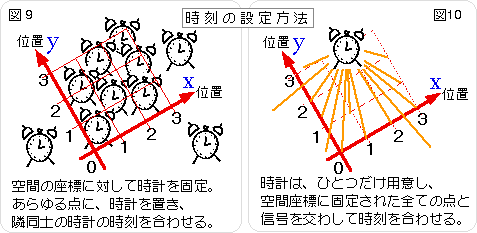
時刻の概念としては、図９の方が、わかりやすいと思います。しかし、実際に「時計を見る」という作業は図10の方になっています。歪んだ時空を考えるのでなければ、どちらも同じものだと考えて差し支え在りません。
時間と空間
時間の存在は、「出来事」と切り放して考えることはできません。また、空間と違う点は、向きがあるという事です。原因の後に結果が在ります。覆水盆に返らず。つまり、順番が重要です。これらの出来事を連ねてグラフにすると見やすくなります。点の運動などは、曲線を描いて一目瞭然。グラフから、点の運動に戻すためには、スリットを用意してみてください。幅２mm程が適当でしょうか。スリットをグラフの空間方向と平行に置き、時間軸の方向へゆっくり移動させていきます。すると、すき間の中で、点が動いているのが見えるでしょう。
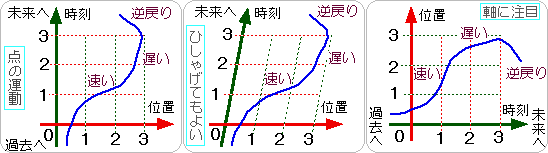
なお、これはあくまでもグラフでしかないので、空間のｘ軸とｙ軸といったような場合と異なり、空間の軸と時間の軸を垂直に描かなければならないという必要はありません。単に、見やすくするために、そうしているだけにすぎません。上の図は、どれも同じ内容を表しています。どれを使ってもかまいません。
うそつきは宇宙のはじまり
宇宙の初めの時間は虚時間 ( imaginary time) だったという話があります。虚時間とは、その時刻の値を２乗すると、マイナスの数になるという、架空の時間です。もともと計算上の便宜として使われていました。ホーキング ( Stephen W. Hawking 1942- ) は、宇宙の始まりに関する理論の問題を解決するために、この虚時間を積極的に導入しました（文献４）。また、ワームホール（宇宙の近道）などを作ったり、宇宙を２つに引きちぎったりするような、時空の構造の変わり目でも、時間が虚時間になるとも考えられています（文献５）。座標の系
物理的な対象物に、座標をくっつけた全体を、「座標系 (coordinate system) 」と呼びます。 ところで、「系 (system)」とは何でしょう？ 辞書で引いてみましょう。「 (いとすじの意) １、深い関係で次つぎとつながっている。・・・」（三省堂新明解国語事典から抜粋引用）とあります。つまり、互いにかかわり合いのあるもののひとまとまりを意味します。 以上、手短に直感的にまとめると、- 座標系 (coordinate system) とは、
物理的な土台の上に座標を張り付けたもの。
2-2-3、遊園地にいこう
「バンジージャンプ」にトライしたことはありますか？。「フリーフォール」だとか、「バイキング」だとかに乗ってみたことはありますでしょうか？ 一瞬の間ですが、体がフワッと軽くなります。本当に体の重さがなくなってしまいます。ためしに、軽いボールなどを持ち込んでみましょう。短い時間ですが、手を離しても、手元でフワッと浮くはずです。遊園地に行く金が無くても、体育館にトランポリンがあれば、飛び跳ねながら、同じような実験が出来るはずです。このときの実験のコツは、ボールと一緒に、出来るだけ遠くを眺めてみてください。地平線なんか在ったら、それがいちばんいいです。
さらに、その浮いているボールに、少しだけ速度を与えてみましょう。一定の速度で、あなたの手許を、まっすぐに移動して行くはずです。トランポリンを使って実験する場合には、ボールは他の人にタイミングを見計らって投げてもらい、あなたは、視線を遥かかなた遠くへと向けておきます。大きな鏡を立てかけて、自分の目を見ながら跳ぶという方法もあるでしょう。
自分も含めて、いろいろなものと一緒に落下してみた世界は、重力を感じない世界です。何者からも力を受けていない世界と、ほとんど同じです。ここでは「慣性の法則＝全ての物体は、それになんらの力を加えない限り、いつまでも静止の状態、又は速度一定の等速直線運動を続ける。」を実感できるでしょう。
では、ボールの代わりに、大きな定規を投げてみましょう。ただし、定規を回転させてはいけません。すると、この定規を使って、ものの位置を、数字で表すことが出来るようになります。つまり、座標系が出来ました。そして、あなたと一緒に飛んでいるその定規は、あなたに対して、止まっているか、または、一定の速度で移動して行くはずです。定規とボールを同時に投げると、やはり、ボールは定規に対して、一定の速度で進んでいきます。この、慣性の法則の成り立つ世界の定規で定められた座標系のことを、「慣性系」とよびます。
（なお、あまり調子に乗って、その手の乗り物に乗りすぎると、とても気持ちが悪くなるので気おつけましょう。）
実は、遊園地に行ったり、飛び跳ねたりしなくても、便宜的な慣性系は存在します。上下方向について目をつぶることにすれば、私たちのいる地上は、重力の方向と垂直な水平方向には、だいたい慣性の法則が成り立っていると考えてよいでしょう。水平ですべすべの机の上に、ドライアイスを砕いて置いてみます。少し待ってから、指ではじくと、気持ちいいくらい一定の速度で滑っていきます。つまり、これらは止まっているか、一定の速度で運動し続けるかのどちらかに見えます。この机に、定規で物体の位置を読みとるための目盛をふれば、「慣性系」の出来上がりです。（ただし、机や空気との摩擦が無いわけではないので、厳密には一定の速度にはなりません。）
以上、標語にまとめると、
- 慣性系 ( inertial system) とは、ニュートンの「慣性の法則」が
成り立っているような座標系のことをいう。
2-2-4、ガリレイ変換
あなたは今、天気の良い空を飛んでいる飛行機に乗っているとします。飛行機は順調に水平飛行を続け、気流は穏やかで、エンジンの音以外には、揺れも振動も何もないとしましょう。海水面に対して、高度10000m を保ち、時速800km でまっすぐ飛び続けているとします。さて、窓は全部閉め切っておいて、離陸したことは気絶していて知らなかった事にします。すると、飛んでいるのか、地上にいるのか、区別が付きますでしょうか？ つかないはずです。
そこに、目盛をふった平らなテーブルとドライアイスのセットを持ち込んだら、実験室で行ったのと、全く同じ状況が再現されるでしょう。つまりそこでも水平方向に慣性系が存在しています。そればかりか、全ての力学の実験は、地上で止まっている場合と同じ結果を導くでしょう。なぜそうなるのでしょうか？ それはわかりません。しかし、最も基本的な事実です。だから「原理」です。これが、ガリレイ・ニュートンの相対性原理の内容です。（ガリレイの時代には、飛行機はなかったので、ガリレイは一定の速さで進む船を例に出して、説明していたようです。近年は、船ではなくて、電車がよく登場します。） 慣性系は、無数に存在し、どれか一つが絶対的な基準であるとすることは出来ません。つまり、慣性系同士は、他を見て初めて己を知る「相対的」な存在なのです。だから、「相対性原理」と呼ばれています。なお、ガリレイの心づもりとしては、この原理は、全ての物理法則に対して成り立つものと考えていたのと、私は思います。しかし、当時は電気と磁気の法則が、まだ明らかになっていなかったので、その点は考慮されていなかったようです。そのため後の人たちによって「全ての『力学の』法則は」という、制限付きの原理とみなされるようになりました。
では、異なる慣性系同士の関係は、どの様にして記述しましょうか。つまり、慣性系は、座標系の一種でしたから、物理的な対象の各点に座標の数値を割り振ってあります。同じモノを２つの慣性系で眺めるとき、同じモノなのに、座標の値は異なります。この２つの座標の値の間の関係が明らかになっていれば、どちらの座標も好みに応じて使い分けられるということになります。これはガリレイ変換と呼ばれています。変換とは、取り替えることを意味します。
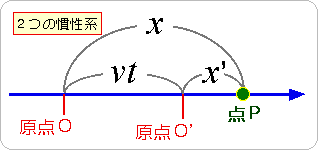
簡単のために、空間一次元の場合について考えます。同じ線上に、２つの慣性系があり、時刻
この座標値の入れ替えの関係式を「ガリレイ変換」といいます。
次に、速度の合成則を導きます。点Ｐが、原点O’の置かれた慣性系に対して、速度ｕで移動していたとしましょう。すると、点Ｐの位置は、ｐoを定数として、
この章のチェックポイント
以下の用語を、他人に説明してみましょう。- 慣性の法則
- 座標
- 慣性系
- ガリレイ・ニュートンの相対性原理
- ガリレイ変換
- ガリレイの速度合成則
注意！＜＜訂正＞＞
「慣性の法則」「慣性系」「相対性原理」については、訂正があります。ここもご覧ください。